Travail ciblé sur les nouveaux calculs en terminale

Aperçu des sections

• 

  Généralités

  • 
    

    

    Marquer comme terminé
  • port Contenu interactif

    Marquer comme terminé
• 

  Travailler avec les unités

  • Exemples en chimie : retrouver une formule oubliée
    

    \(R= 8,31 Pa.m^3mol^{-1}K^{-1} \Longrightarrow R = \)

    \( R= \frac{Pa.m^3}{mol.K} = \frac{P.V}{n.T} \Longrightarrow P.V = n.R.T \)

    \(\rho (H_2O) = 1000 g/L \Longrightarrow \rho = \)

    \( \rho (\frac{g}{L}) = \frac{m}{V}\)

    \(M(O) = 16.0 g/mol \Longrightarrow M = \)

    \(M (\frac{g}{mol}) = \frac{m}{n} \Longrightarrow m = M \times n \)

    \(V_m = 24 L/mol \Longrightarrow V_m = \)

    \(V_m (\frac{L}{mol}) = \frac{V}{n} \Longrightarrow V = V_m \times n \)

    \(C_0 = 1,0 mol/L \Longrightarrow C = \)

    \(C (\frac{mol}{L}) = \frac{n}{V} \Longrightarrow n = C \times V \)

    \(C_m = 3,0 g/L \Longrightarrow C_m = \)

    \(C_m (\frac{g}{L}) = \frac{m}{V} \Longrightarrow m = C_m \times V \)

    Marquer comme terminé
• 

  Travailler sur des résolutions de problèmes.

  • Révisions des règles de calcul

    

    

    

    

    

    
    

    

    
    

    

    

    

    

    

    

    

    

    

    

    

    
    

    

    

    

    

    

    

    

    
    

    

    

    
    

    

    

    

    

    

    

    

    Previous Next
  • On dispose d’un volume V de 30 mL de vinaigre ménager à 12 °. Le vinaigre ménager à 12 ° est une solution aqueuse d’acide éthanoïque qui contient 12 g d’acide éthanoïque pour 100 g de solution.
    Données:
    ‒masse molaire moléculaire \( M(CH_3COOH) = 60,0 g.mol^{-1} \)
    ‒masse volumique à 20 °C ρ(vinaigre) = 1,010 g/mL
    Calculer la concentration molaire \( [CH_3COOH] \)

    APP : surligner APP : extraire et unités Ana : trouver l'ordre des calculs Réa C : Calculer Réa C : Substituer

    On disposed’un volume V de 30 mL de vinaigre ménager à 12 °. Le vinaigreménager à 12 ° est une solution aqueuse d’acide éthanoïque quicontient 12 g d’acide éthanoïque pour 100 g de solution.
    Données: ‒masse molaire moléculaire \( M(CH_3COOH) = 60,0 gmol.L^{-1} \)
    ‒masse volumique à 20 °C ρ(vinaigre) = 1,010 g/mL
    Calculer la concentration molaire \( [CH_3COOH] \)  

    Extraction des données :

    \( V_{vinaigre} \) = 30 mL
    \( M(CH_3COOH) \) = 60,0 g/mol = \( \frac{m_{CH_3COOH}}{n_{CH_3COOH}} \)
    ρ(vinaigre) = 1,010 g/mL =\( \frac{m_{vinaigre}}{V_{vinaigre}} \)
    \( P = \frac{12}{100} = \frac{m_{CH_3COOH}}{m_{vinaigre}} \)
    \( [CH_3COOH] en mol/L = \frac{n_{CH_3COOH}}{V_{vinaigre}}\)

    Trouver l'ordre des étapes :

    \( \color{red}{V_{vinaigre}} \) = 30 mL1
    \( M(CH_3COOH) \) = 60,0 g/mol = \( \frac{m_{CH_3COOH}}{n_{CH_3COOH}} \)4
    ρ(vinaigre) = 1,010 g/mL = \( \frac{\color{blue}{ m_{vinaigre}}}{\color{red}{ V_{vinaigre} }} \)2
    \( P = \frac{12}{100} = \frac{m_{CH_3COOH} }{\color{blue}{m_{vinaigre}}} \) 3
    \( [CH_3COOH] en mol/L = \frac{n_{CH_3COOH}}{V_{vinaigre}}\)5

    Calculer :

    1\(V_{vinaigre} \) = 30 mL = 0,030 L
    2\( m_{vinaigre}= ρ(vinaigre)\times V_{vinaigre} = 1,010 g/mL \times 30 mL = 30,3 g \)
    3\( m_{CH_3COOH} = \frac{12}{100} \times m_{vinaigre} =0,12 \times 30,3 = 3,636 g \)
    4 \( n_{CH_3COOH} = \frac{m_{CH_3COOH}}{M(CH_3COOH)} = \frac{3,636}{60}= 0,0606 mol \)
    5\( [CH_3COOH] en mol/L = \frac{n_{CH_3COOH}}{V_{vinaigre}}= \frac{0,0606 mol}{0,030 L} = 2,0 mol/L\)

    Exprimer puis calculer :

    1\(V_{vinaigre} \)
    2\( m_{vinaigre}= ρ(vinaigre)\times V_{vinaigre} \)
    3\( m_{CH_3COOH} = \frac{12}{100} \times m_{vinaigre} =\frac{12}{100} ρ(vinaigre)\times V_{vinaigre} \)
    4 \( n_{CH_3COOH} = \frac{m_{CH_3COOH}}{M(CH_3COOH)} = \frac{\frac{12}{100} ρ(vinaigre)\times V_{vinaigre}}{M(CH_3COOH)} \)
    5\( [CH_3COOH] = \frac{n_{CH_3COOH}}{V_{vinaigre}}= \frac{\frac{12}{100} \times ρ(vinaigre)\times V_{vinaigre}}{M(CH_3COOH).V_{vinaigre}}\)
    \( [CH_3COOH] = \frac{\frac{12}{100} \times ρ(vinaigre)}{M(CH_3COOH)}= \frac{\frac{12}{100} \times 1010g/L}{60g/mol} = 2,0 mol/L\)

    Marquer comme terminé
  • La société française ENGIE investit dans le développement d’un des premiers projets de dihydrogène renouvelable. Ce projet est situé dans la région de Pilbara en Australie. En 2024, la première phase produira 640 tonnes de dihydrogène par an. Le dihydrogène sera utilisé comme matière première pour la production d'ammoniac. Le rendement de la production d’ammoniac sera de 20 %.
    Données:
    ‒masses molaires atomiques en g·mol-1 : M(H) = 1,0 ; M(N) = 14,0.
    Déterminer la masse d’ammoniac qui pourra être produite en 2024 à partir du dihydrogène produit dans l’usine de Pilbara.
    
    

    APP : surligner APP : extraire et unités Ana : trouver l'ordre des calculs Réa C : Calculer Réa C : Substituer

    La société française ENGIE investit dans le développement d’un des premiers projets de dihydrogène renouvelable. Ce projet est situé dans la région de Pilbara en Australie. En 2024, la première phase produira 640 tonnes de dihydrogène par an. Le dihydrogène sera utilisé comme matière première pour la production d'ammoniac. Le rendement de la production d’ammoniac sera de 20 % .
    Données: masses molaires atomiques en g·mol-1 : M(H) = 1,0 ; M(N) = 14,0
    Image : réactifs \(N_2 + H_2\) produit \(NH_3 \)

    Extraction des données :

    \( m_{H_2} \) = 640 t
    équation équilibrée : \( 2N_2 + 3H_2 \longrightarrow 2NH_3 \)
    \( M(NH_3) \) = 17 g/mol = \( \frac{m_{NH_3}}{n_{NH_3}} \)
    \( M(H_2) \) = 2 g/mol = \( \frac{m_{H_2}}{n_{H_2}} \)
    \( r = \frac{20}{100} = \frac{m_{exp}(NH_3)}{m_{max}(NH_3)} \)
    

    Trouver l'ordre des étapes :

    \( \color{red}{m_{H_2}} = 640 t = 640.10^6 g \)1
    \( 2N_2 + 3H_2 \longrightarrow 2NH_3 \)
    donc si on utilise tout le dihydrogène :
    \( \frac{n_{H_2}}{3}=\frac{\color{blue}{n_{max}(NH_3)}}{2} \)3
    \( M(NH_3) \) = 17,0 g/mol = \( \frac{m_{NH_3}}{\color{blue}{n_{NH_3}}} \)4
    \( M(H_2) \) = 2 g/mol = \( \frac{m_{H_2}}{\color{blue}{n_{H_2}}} \)2
    \( r = \frac{20}{100} = \frac{\color{blue}{m_{exp}(NH_3)}}{m_{max}(NH_3)} \) 5
    

    Calculer :

    1\( m_{H_2} = 640 t = 640.10^6 g \)
    2\( n_{H_2}= \frac{m_{H_2}}{M_{H_2}} = \frac{640.10^6}{2} = 320.10^6 mol \)
    3\( n_{max}(NH_3)= \frac{2 \times n_{H_2}}{3}= 320.10^6\times 2/3 = 213.10^6 mol \)
    4 \( m_{max}(NH_3) = n_{max}(NH_3) \times M_{NH_3} = 213.10^6 mol \times 17 = 3,63.10^9 g \)
    5\( \frac{20}{100} \times m_{max}(NH_3) = m_{exp}(NH_3) = 0,2\times 3,63.10^9 = 7,25.10^8 g = 725 t \)

    Exprimer puis calculer :

    1\( m_{H_2} = 640 t = 640.10^6 g \)
    2\( n_{H_2}= \frac{m_{H_2}}{M_{H_2}} \)
    3\( n_{max}(NH_3)= \frac{2 \times n_{H_2}}{3}= \frac{2 \times m_{H_2}}{3\times M_{H_2} } \)
    4 \( m_{max}(NH_3) = \frac{2 \times m_{H_2}}{3\times M_{H_2} }\times M_{NH_3} \)
    5\( \frac{20}{100} \times m_{max}(NH_3) = m_{exp}(NH_3) = 0,2 \times \frac{2 \times m_{H_2}}{3\times M_{H_2} }\times M_{NH_3} = 0,2 \times \frac{2 \times 640.10^6}{3\times 2 }\times 17 =7,25.10^8 g = 725 t \)

    Marquer comme terminé
  • Pour se débarrasser de la couche de calcaire d’épaisseur moyenne de 5 μm qui s’est déposée sur la paroi vitrée d’une douche,on dispose d’un volume V de 30 mL de vinaigre à 2 mol/L. Le calcaire qui se dépose sur la vitre provient de l’eau du robinet.Le calcaire est un solide ionique de formule \( CaCO_{3(s)} \). Il réagit totalement avec les ions oxonium, libérés par l’acide éthanoïque,selon la transformation chimique modélisée par l’équation de réaction suivante:
    \( 2 H_3O^+_{(aq)} + CaCO_{3(s)} \longrightarrow Ca^{2+}_{(aq)} + CO_{2(g)} + 3 H_2O \)
    On considèrera aussi lors de cette réaction tous les molécules d'acide éthonoïques réagissent pour libérer un proton, selon l'équation :
    \( CH_3COOH_{(aq)} + H_2O_{(l)} \longrightarrow H_3O^+_{(aq)} + CH_3COO^-_{(aq)} \)
    Données:
    ‒masse molaire moléculaire \( M(CaCO_3) = 100,1 g/mol \);
    ‒massevolumique à 20 °C \(ρ(CaCO_3) = 2,65×10^3kg·m^{-3}\);
    ‒dimension de la paroi de douche:110 cm × 200 cm
    Déterminer si le volume de vinaigre sera suffisant pour éliminer tout le calcaire.

    APP : extraire et unités Ana : trouver l'ordre des calculs Réa C : Calculer

    Extraction des données :

    vinaigre : V = 30 mL et C = 2 mol/L c = \( \frac{n_{CH_3COOH}}{V} \)
    ‒masse molaire moléculaire \( M(CaCO_3) = 100,1 \) g/mol = \( \frac{m_{CaCO_3}}{n_{CaCO_3}} \)
    ‒massevolumique à 20 °C \(ρ(CaCO_3) = 2,65×10^3kg·m^{-3}\)= \( \frac{m_{CaCO_3}}{V_{CaCO_3}} \)
    ‒dimension de la paroi de douche:110 cm × 200 cm = 1,10 m x 2,00 m
    épaisseur moyenne de \( 5 μm = 5.10^{-6} m \) \( V_{calcaire} = l \times L \times h \)
    \( CH_3COOH_{(aq)} + H_2O_{(l)} \longrightarrow H_3O^+_{(aq)} + CH_3COO^-_{(aq)} \)
    \( \frac{n_{CH_3COOH}}{1} = \frac{n_{H_3O^+}}{1} \)
    \( 2 H_3O^+_{(aq)} + CaCO_{3(s)} \longrightarrow Ca^{2+}_{(aq)} + CO_{2(g)} + 3 H_2O \)
    \( \frac{n_{CaCO_{3(s)}}}{1} = \frac{n_{H_3O^+}}{2} \)
    

    Trouver l'ordre des étapes :

    vinaigre : V = 30 mL et C = 2 mol/L c = \( \frac{n_{CH_3COOH}}{V} \)1
    \( CH_3COOH_{(aq)} + H_2O_{(l)} \longrightarrow H_3O^+_{(aq)} + CH_3COO^-_{(aq)} \)
    \( \frac{n_{CH_3COOH}}{1} = \frac{n_{H_3O^+}}{1} \) 2
    \( 2 H_3O^+_{(aq)} + CaCO_{3(s)} \longrightarrow Ca^{2+}_{(aq)} + CO_{2(g)} + 3 H_2O \)
    \( \frac{n_{CaCO_{3(s)}}}{1} = \frac{n_{H_3O^+}}{2} \) 3
    ‒dimension de la paroi de douche:110 cm × 200 cm = 1,10 m x 2,00 m
    épaisseur moyenne de \( 5 μm = 5.10^{-6} m \Longrightarrow V_{CaCO_3} = lxLxh\)1
    ‒massevolumique à 20 °C \(ρ(CaCO_3) = 2,65×10^3kg·m^{-3}\)= \( \frac{m_{CaCO_3}}{V_{CaCO_3}} \) 2
    ‒masse molaire moléculaire \( M(CaCO_3) = 100,1 \) g/mol = \( \frac{m_{CaCO_3}}{n_{CaCO_3}} \)3
    

    Calculer :

    1 V = 30 mL et C = 2 mol/L n = C x V = 2 x 0,030 = 0,060 mol \)
    2 \( n(H_3O^+) = n(CH_3COOH) = 0,060 mol \)
    3 \( n(CaCO_{3(s)}) = \frac{n(H_3O^+)}{2}=\frac{0,060}{2}=0,030 mol \)
    Avec le vinaire on peut éliminer 0,060 mole de calcaire.
    1 \( V_{CaCO_3} = lxLxh = 5.10^{-6} m x 1,10 m x 2,00 m = 1,1.10^{-5} m^3 \)
    2 \( m_{CaCO_3} = ρ(CaCO_3) \times V_{CaCO_3} = 2,65×10^3kg·m^{-3} x 1,1.10^{-5} m^3 = 0,029kg = 29 g \)
    3 \( n_{CaCO_3} = \frac{m_{CaCO_3}}{M_{CaCO_3}}=\frac{29}{100,1} \)= 0, 29 mol >> 0,060 mol
    Il n'y a pas assez de vinaigre car au mieux 0,060 mol sur les 0,29 seront consommés.

    Marquer comme terminé
• 

  Travailler avec des log, des puissances, des exponentielles

  • Révisions des règles de calcul

    

    

    

    

    

    

    

    

    

    

    

    
    

    

    

    

    

    Previous Next
  • test d'expressions littérales sur ces fonctions

    Marquer comme terminé
  • Exemples en chimie :

    \(K_A= 10^{-pK_A} \Longrightarrow pK_A = \)

    \( -pK_A=log K_A \Longrightarrow pK_A=-log K_A\)

    \([H_3O^+]= C^0 \times 10^{-pH} \Longrightarrow pH = \)

    \( \frac{[H_3O^+]}{C^0}= 10^{-pH} \Longrightarrow pH=-log \frac{[H_3O^+]}{C^0}\)

    \(pH = pK_A + log \lgroup \frac{[A^-]}{[HA]} \rgroup \Longrightarrow \frac{[A^-]}{[HA]} = \)

    \(pH = pK_A + log \lgroup \frac{[A^-]}{[HA]} \Longrightarrow pH - pK_A = log \lgroup \frac{[A^-]}{[HA]} \) On utilise la puissance de 10 : \(10^{pH - pK_A} = \frac{[A^-]}{[HA]}\)

    Marquer comme terminé
  • Exemples en chimie :

    \(pK_A=-log K_A \Longrightarrow K_A = \)

    \(K_A= 10^{-pK_A} \)

    \(pH=-log \frac{[H_3O^+]}{C^0} \Longrightarrow [H_3O^+] = \)

    \([H_3O^+]= C^0 \times 10^{-pH} \)

    \(K_A=\frac{[A^-]\times [H_3O^+]}{[HA] \times C^0} \Longrightarrow pK_A = \)

    \(pK_A= -log K_A= -log \lgroup \frac{[A^-]\times [H_3O^+]}{[HA] \times C^0} \rgroup\) or \(log(a \times b)=log a + log b\) avec \(a= \frac{[A^-]}{[HA]}\) et \(b = \frac{[H_3O^+]}{C^0}\) \(pK_A= -log \lgroup \frac{[A^-]}{[HA]} \rgroup -log \lgroup \frac{[H_3O^+]}{C^0} \rgroup = -log \lgroup \frac{[A^-]}{[HA]} \rgroup + pH \)

    Marquer comme terminé
  • Exemples avec le niveau d'intensité sonore

    \(L=10\times log \frac{I}{I_0} \Longrightarrow I = \)

    \(I= I_0 \times 10^{\frac{L}{10}} \)

    \(Absorbtion A=L_{sortie}-L_{entrée} \Longrightarrow A=f( I_{sortie} , I_{entrée})= ... \)

    \(L=10\times log \frac{I}{I_0} \) donc \(A=10\times log \frac{I_{sortie}}{I_0}-10\times log \frac{I_{entrée}}{I_0}\) factorisation : \(A= 10\times(log \frac{I_{sortie}}{I_0}-log \frac{I_{entrée}}{I_0})\) log(a)-log(b) = log(a/b) : \(A= 10\times(log \frac{I_{sortie}}{I_0} ÷ \frac{I_{entrée}}{I_0})\) log(a)-log(b) = log(a/b) : \(A= 10\times(log \frac{I_{sortie}}{I_0} \times \frac{I_0}{I_{entrée}}) = 10\times log \frac{I_{sortie}}{I_{entrée}} \)

    On double les sources \( I'=2I \Longrightarrow L'=f(L)= ... \)

    \(L=10\times log \frac{I}{I_0} \) \(L'=10\times log \frac{2\times I}{I_0}\) log(axb) =log(a)+log(b) : \(L'=10\times (log (2) + log \frac{I}{I_0})\) On développe : \( L'=10\times log (2) + 10\times log \frac{I}{I_0}= 10\times log (2) + L = 3dB +L \)

    On double la distance d \( I'=\frac{I}{4} \Longrightarrow L'=f(L)= ... \)

    \(L=10\times log \frac{I}{I_0} \) \(L'= 10\times log \frac{I'}{I_0} = 10 \times log \frac{I}{4\times I_0} \) log(axb) =log(a)+log(b) : \( L'=10 \times (log \frac{1}{4} + log \frac{I}{I_0} )\) On développe : \( L'=10\times log \frac{1}{4} + 10\times log \frac{I}{I_0}= 10\times log \frac{1}{4} + L = -6dB + L \)

    \( I=\frac{P}{2.\pi .d^2} L=10\times log \frac{I}{I_0} \Longrightarrow d=f(P,L,I_0)= ... \)

    \(L=10\times log \frac{I}{I_0} \Longrightarrow L = 10\times log \frac{P}{2.\pi .d^2.I_0} \) On élimine la fonction log : \(\frac{L}{10}= log \frac{P}{2.\pi .d^2.I_0} \Longrightarrow 10^{\frac{L}{10}} = \frac{P}{2.\pi .d^2.I_0} \) \( d^2=\frac{P}{2.\pi .10^{\frac{L}{10}} .I_0} \) On prend la racine de l'égalité : \( d=\sqrt{ \frac{P}{2.\pi .10^{\frac{L}{10}} .I_0}} \)

    Marquer comme terminé
  • Exemples en nucléaire

    \( \frac{N_0}{2} = N_0.e^{- \lambda \times t_{1/2}} \Longrightarrow \lambda = f(t_{1/2}) \)

    \( N(t) = N_0.e^{- \lambda \times t} \Longrightarrow t = ...\)

    \( \frac{N_0}{2} = N_0.e^{- \lambda \times t_{1/2}} \)

    Simplifier :

    \( \frac{1}{2} = e^{- \lambda \times t_{1/2}} \)

    On applique la fonction ln :

    \( ln( \frac{1}{2} ) = - \lambda \times t_{1/2} = -ln(2)\)

    On réorganise les facteurs :

    \( \lambda = \frac{ln(2)}{t_{1/2}} \)

    \( \lambda = \frac{ln(2)}{t_{1/2}} ) \)

    \( N(t) = N_0.e^{- \lambda \times t} \)

    On isole la fonction exponentielle :

    \( \frac{N(t)}{N_0} = e^{- \lambda \times t} \)

    On applique la fonction ln :

    \( ln( \frac{N(t)}{N_0} ) = - \lambda \times t \)

    On réorganise les facteurs :

    \( \frac{-1}{\lambda} \times ln( \frac{N(t)}{N_0} ) = t \)

    \( t = \frac{1}{\lambda} \times ln( \frac{N_0}{N(t)} ) \)

    Marquer comme terminé
  • Exemples en chimie avec ln et exp:

    \([S]= [S_0]\times e^{-k.t} \Longrightarrow ln([S] = \)

    \( [S]= [S_0]\times e^{-k.t} \Longrightarrow ln([S]) = ln([S_0]\times e^{-k.t} ) = ln([S_0]) + ln( e^{-k.t} )= ln([S_0]) - k.t \)

    \(\frac{[S_0]}{2}= [S_0]\times e^{-k.t_{1/2}} \Longrightarrow t_{1/2} = f(k)\)

    \(\frac{[S_0]}{2}= [S_0]\times e^{-k.t_{1/2}} \) On isole la fonction exp : \(\frac{1}{2}= e^{-k.t_{1/2}} \) On prend le ln de l'expression : \(ln(\frac{1}{2})= ln(e^{-k.t_{1/2}})= -k.t_{1/2} = -ln(2) \) On divise par -k :

    \( t_{1/2} = \frac{ln(2)}{k} \)

    \([S](t) = [S_0]\times e^{-k.t} \Longrightarrow t = ...\)

    \([S]= [S_0]\times e^{-k.t} \) On isole la fonction exp : \(\frac{[S]}{[S_0]}= e^{-k.t} \) On prend le ln de l'expression : \(ln(\frac{[S]}{[S_0]} )= ln(e^{-k.t_{1/2}} )= -k.t \) On divise par -k :

    \( t_{1/2} = \frac{1}{-k}.ln(\frac{[S]}{[S_0]} ) \)

    Marquer comme terminé
• 

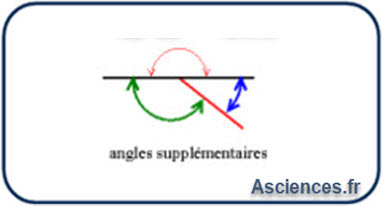
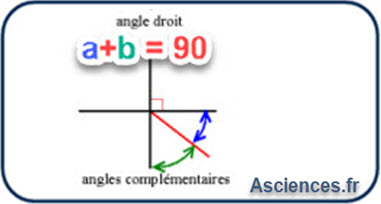
  Travailler avec des angles, les démonstrations sur les ondes, l'optique...

  • Révisions des règles de calcul

    
    

    

    

    

    

    

    

    

    

    

    

    
    

    
    

    

    

    

    

    

    

    

    

    

    

    

    Previous Next
  • 

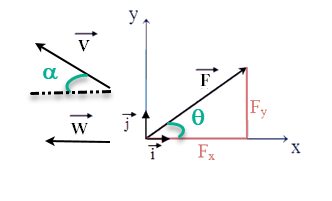
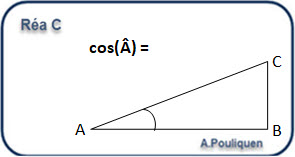
    Coordonnées de \( \vec{F} \) Coordonnées de \( \vec{V} \) Coordonnées de \( \vec{W} \) Norme de \( F = || \vec{F}|| = f(F_x,F_y) \) Angle \( \theta = f(F_x,F_y) \)

    Cours:

    \( \vec{F} =\binom{F_X = F\times cos(\theta) }{F_Y = F\times sin(\theta)} \)

    Cours:

    \( \vec{V} =\binom{V_X = - V\times cos(\theta) }{V_Y = V\times sin(\theta)} \)

    Cours:

    \( \vec{W} =\binom{W_X = - W }{W_Y = 0} \)

    Cours:

    \( \vec{F} =\binom{F_X = F\times cos(\theta) }{F_Y = F\times sin(\theta)} \) \( F =\sqrt{F_X^2 + F_Y^2} \)

    Cours:

    \( \vec{F} =\binom{F_X = F\times cos(\theta) }{F_Y = F\times sin(\theta)} \) \( \frac{F_Y}{F_X} = tan(\theta) \)

    Marquer comme terminé
  • 

    On utilise un laser de longueur d'onde 630 nm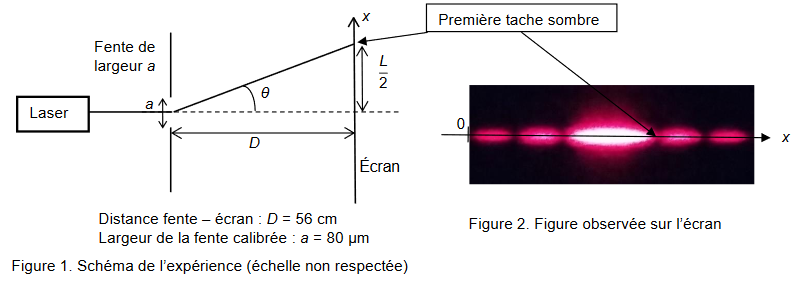
    

    Rappeler la relation de la diffraction Déterminer L

    Cours:

    \( \theta = \frac{\lambda}{a} \) Donc si a est plus petit alors la diffraction est plus forte.

    trigonométrie:

    \( tan( \theta) = \frac{oppose}{adjacent} = \frac{L/2}{D} = \frac{L}{2.D} \) Or : \( \theta \approx tan( \theta) = \frac{L}{2.D} = \frac{\lambda}{a}\) Donc : \( L = \frac{2.D.\lambda}{a} = \frac{2 \times 0,56 \times 630.10^{-9}}{80.10^{-6}} = 8,8.10.10^{-3} \) Le résultat est réaliste : 8,8 mm

    Marquer comme terminé
  • 

    On utilise un laser de longueur d'onde 635 nm et on obtient L = 45 mm pour D = 350 mm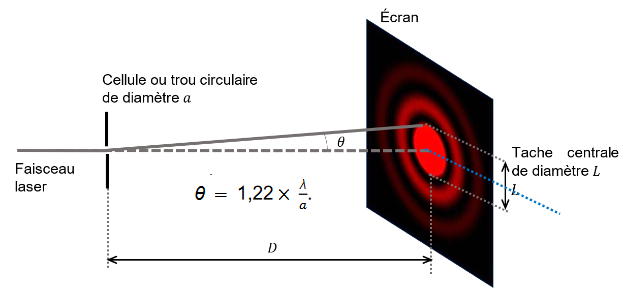
    

    Déterminer a

    D'après le texte :

    \( \theta = \frac{1,22\times \lambda}{a} \)

    Trigonométrie :

    \( tan( \theta) = \frac{oppose}{adjacent} = \frac{L/2}{D} = \frac{L}{2.D} \) Or : \( \theta \approx tan( \theta) = \frac{L}{2.D} = \frac{1,22\times \lambda}{a}\) Donc : \( a = \frac{2.D \times 1,22\times \lambda}{L} = \frac{2,44 \times 0,350 \times 635.10^{-9}}{45.10^{-3}} = 1,2.10^{-5} m \)

    Marquer comme terminé
  • OBSERVATION ORNITHOLOGIQUE D’UNE OIE CENDRÉE (Métropole Sept 2023)

    

    On travaille avec l'hypothèse : D >> b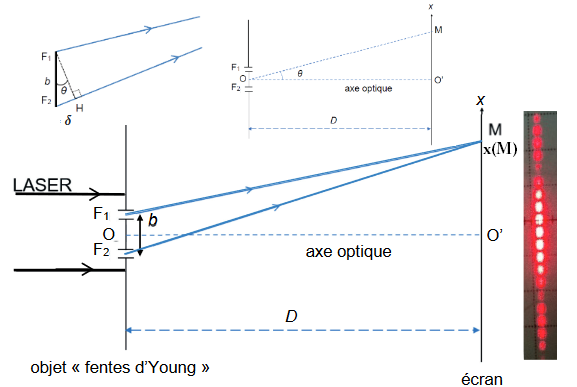
    

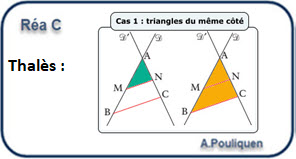
    Exprimer \( \theta \) dans les deux triangles Exprimer la différence de chemin optique \( \delta = F_2H \) Exprimer x pour \( \delta = k \times \lambda \) Exprimer interfrange : i = x(k+1) - x(k)

    trigonométrie :

    \( \theta \approx sin( \theta) = \frac{oppose}{hypoténuse} = \frac{F_2H}{F_1F_2} \) \( \theta \approx tan( \theta) = \frac{oppose}{adjacent} = \frac{x(M)}{D} \)

    les deux angles sont égaux donc :

    \( \theta \approx \frac{x(M)}{D} = \frac{F_2H}{F_1F_2} = \frac{\delta }{b} \) Sortir la différence de chemin optique dans l'air : \( \frac{x(M) \times b}{D} = \delta \)

    condition d'interférences constructives :

    \( \delta = k \times \lambda \) Exprimons x(k) : \( x(M) = \frac{ \delta \times D}{b} = \frac{ k \times \lambda \times D}{b} \)

    interfrange : i = x(k+1) - x(k) :

    i = x(k+1) - x(k) = \( \frac{ (k+1) \times \lambda \times D}{b} - \frac{ k \times \lambda \times D}{b} =\frac{ 1 \times \lambda \times D}{b} \)

    Marquer comme terminé
  • 

    Données :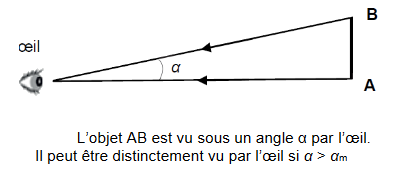
    la distance minimale entre Mars et la Terre est de 62,07 millions de kilomètres ;
    à l’œil nu, l’angle sous lequel est vue la Lune est de 0,0090 rad ;
    le diamètre de Mars est de 6 794 km ;
    pouvoir séparateur de l’œil humain : il correspond à l’angle minimal, noté \( \alpha_m \), au-dessus duquel l’œil humain peut différencier deux points. Il a pour valeur \( \alpha_m = 2,9×10^{–4} rad \); pour des angles suffisamment petits, c’est-à-dire très inférieurs à 1 radian, on peut écrire : tan θ = θ (où θ est exprimé en radian).
    Soit une lunette : \( f_1' = 100 cm f_2' = 5 cm \);

    Montrer que la Lune est vue comme un disque Montrer que la Mars est vu comme un point Exprimer \( G=\frac{\alpha '}{\alpha} =f(f_1',f_2') \) Montrer que Mars est visible comme un disque par la lunette

    D'après les données:

    Pour la Lune : 0,0090 rad >> \( 2,9×10^{–4}\) on voit un disque

    Utilisons la tangente pour calculer l'angle :

    \( \alpha \approx tan (\alpha ) = \frac{AB}{D} \) Pour la Mars : \( \alpha = \frac{AB}{D} = \frac{ 6 794 km}{62,07.10^6 km} = 1,1.10^{-4} \) \( 1,1.10^{-4} < 2,9×10^{–4} \) on voit un point, on ne peut pas séparer les différents points de Mars.

    Utilisons la tangente pour calculer l'angle :

    \( \alpha \approx tan (\alpha ) = \frac{A_1B_1}{f_1'} \) \( \alpha ' \approx tan (\alpha ') = \frac{A_1B_1}{f_2'} \) \( G=\frac{\alpha '}{\alpha} = \frac{A_1B_1}{f_2'} \div \frac{A_1B_1}{f_1'} = \frac{A_1B_1}{f_2'} \times \frac{f_1'}{A_1B_1}= \frac{f_1'}{f_2'} = \frac{100'}{5} = 20 \)

    Utilisons le grossissement pour obtenir l'angle après la lunette :

    Pour la Mars : \( \alpha ' = G \times \alpha = 1,1.10^{-4} \times 20 = 2,2.10^{-3} \) \( 2,2.10^{-3} > 2,9×10^{–4} \) on voit un séparer, on peut séparer les différents points de Mars.

    Marquer comme terminé
• 

  Travailler avec des résultats expérimentaux

  • Révisions des règles de calcul

    
    

    

    

    

    

    

    

    

    

    

    
    

    
    

    
    

    

    Previous Next
  • 

    Troisième loi de Képler : \( \frac{T^2 }{R^3} = \frac{4.\pi^2}{G.Ms} \)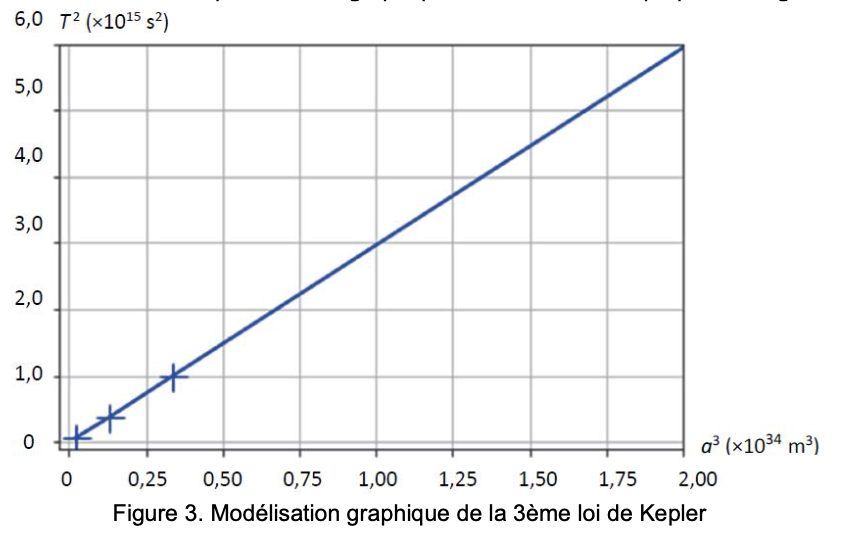

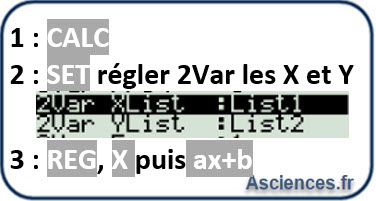
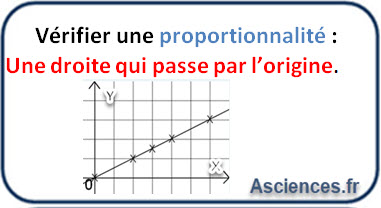
    Déterminer Ms

    Savoir mathématique:

    C'est une droite qui passe par l'origine, les grandeurs sont donc proportionnelles. \( T^2 = C_1 \times R^3 \Longrightarrow \frac{T^2}{R^3} = constante \) On retrouve la troisième loi de Kepler qui est donc vérifiée par ces données expérimentales. La constante de proportionnalité est le coefficient directeur de la droite.

    Savoir mathématique:

    \( C_1 = \frac{y_B - y_A}{x_B - x_A} = \frac{6.10^{15} - 0}{2.10^{34}-0} =3.10^{-19} \)

    On identifie avec l'expression de Képler :

    \( C_1 =\frac{4.\pi^2}{G.Ms} \Longrightarrow Ms =\frac{4.\pi^2}{G.C_1}=\frac{4.\pi^2}{6,67.10^{-11}.3.10^{-19}}=1,97.10^{30} kg\)

    Marquer comme terminé
  • 

    Cinétique d'ordre 1 :la vitesse de disparition Vp d'un réactif est proportionnelle à sa concentration, ici [MMA]  

    Déterminer l'équation de la courbe et montrer que la cinétique est d'ordre 1

    Savoir mathématique:

    C'est une droite qui passe par l'origine, les grandeurs sont donc proportionnelles. \( v_p = C_1 \times [MMA]  \) C'est donc une cinétique d'ordre 1. La constante de proportionnalité C_1 est le coefficient directeur de la droite.

    Savoir mathématique:

    \( C_1 = \frac{y_B - y_A}{x_B - x_A} = \frac{225 mmol/h - 0}{500 mmol/L -0} =0,45\frac{L}{h}  \)  \( v_p = 0,45\times [MMA]  \) 

    Marquer comme terminé
  • 

    la est cinétique d'ordre 1 si \( [S]= [S_0]\times e^{-k.t} \Longrightarrow ln([S]) = ln([S_0]\times e^{-k.t} ) = ln([S_0]) + ln( e^{-k.t} )= ln([S_0])  - k.t  \)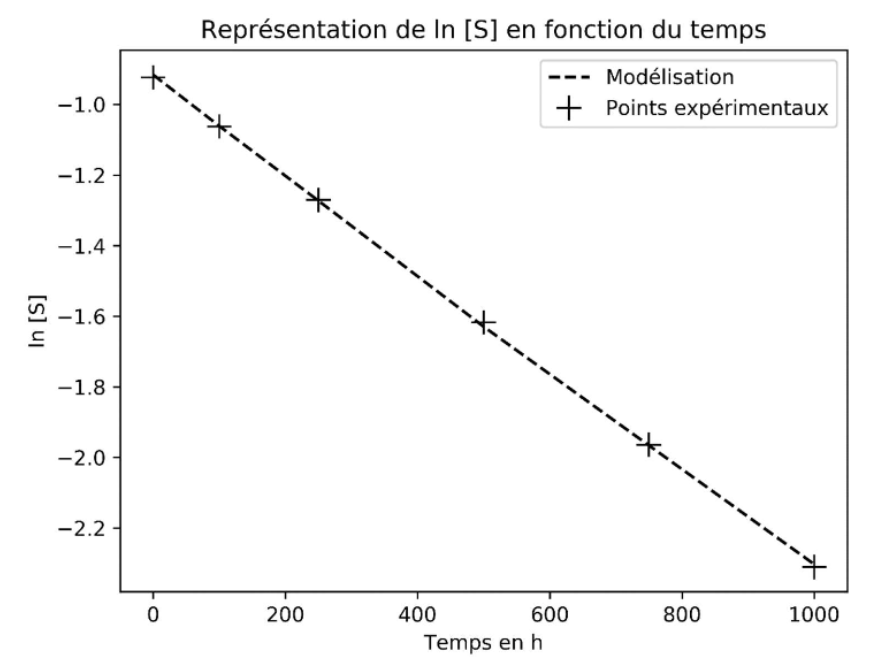

    Déterminer l'équation de la courbe et montrer que la cinétique est d'ordre 1

    Savoir mathématique:

    C'est une droite qui ne passe pas par l'origine y = ax+b.
    ici y = ln[S] et x = t = temps en heure donc : \( ln[S] = b + a \times t  = ln([S_0]) -k.t  \) C'est donc une cinétique d'ordre 1 avec a = -k le coefficient directeur de la droite. De plus b = ordonnée à l'origine \( b = ln([S_0])= -0,9 \)

    Savoir mathématique:

    \( a = -k = \frac{y_B - y_A}{x_B - x_A} = \frac{(-2,3) - (-0,9)}{1000 -0} =-1,4.10^{-3} h^{-1}\) \( ln[S] = -1,4.10^{-3} \times t -0,9  \)

    Marquer comme terminé
  • 

    On a dosé 20mL d'une solution prélevé avec une fiole jaugée et on a obtenu Véq=14 mL avec une solution titrande de concentration \( C_2 = 0,1 mol.L^{-1} \)soit : \( C_0 = 0,70mol.L^{-1} \)
    Informations notées sur l'étiquette : \( C_{m,Ac. Lactique} = 65 g.L^{-1} M_{Ac. Lactique} = 90,1 g.mol^{-1}\)

    Calculer \( U(C_0) \) L'étiquette est-elle correcte ? Proposer des améliorations pour être plus précis

    Savoir utiliser sa calculatrice, les formules sont en général données:

    \( U(C_0) = C_0 \sqrt{(\frac{U(C_2)}{C_2})^2+(\frac{U(Véq)}{Véq})^2+(\frac{U(V_1)}{V_1})^2 }=0,70 \sqrt{(\frac{0,002}{0,1})^2+(\frac{0,25}{14})^2+(\frac{0,03}{20})^2} = 0,03 mol.L^{-1} \) soit : \(C_0 = 0,70 ± 0,03 mol / L.\)

    Comparer les mêmes grandeurs:

    \( C_{0,réf} = \frac{mol}{L} = \frac{g.L^{-1}}{g.mol^{-1}} = \frac{C_{m,Ac. Lactique}}{M_{Ac. Lactique}} = \frac{65}{90,1} =0,72 mol / L \)
    

    Calculons le z-score :

    \( z = \frac{|C_0 - C_{0,réf}|}{U(C_0)} = \frac{|0,70-0,72|}{0,03} = 0,7 <<2 \) c'est en accord avec la valeur de référence.

    Penser aux 3 façons: précisions, grandes valeurs et répétitions

    Il faut :

    • soit répéter l'expérience n fois et faire une moyenne, ce qui est long.
    • soit augmenter les quantités dosées \(Véq \) et \(V_1\) ce qui diminue \(U(C_0)\).
    • soit doser avec du matériel plus précis : diminuer \( U(V_1), U(Véq), U(C_2) \) ce qui diminue \(U(C_0)\).

    Marquer comme terminé
  • 

    Après avoir construit une courbe d'étalonnage : \( \ell = k \times \frac{1}{a} \)
    On mesure la largeur de la tache centrale de diffraction d'un fil de pêche de 0,100 mm.
    

    Calculer graphiquement k Calculer a et U(a) Vérifier la compatibilité du a trouvé Proposer des améliorations pour être plus précis

    Calcul du coefficient directeur de la droite, k :

    \( k = \frac{y_B-y_A}{x_B-x_A} = \frac{0,032 - 0}{19 000 - 0} = 1,68.10^{-6} \)

    Exprimer et calculer a:

    \( \ell = k \times \frac{1}{a} \Rightarrow a = k \times \frac{1}{\ell}= 1,67.10^{-6} \times \frac{1}{0,017} = 9,82.10^{-5} m \)  \( U(a) = a \sqrt{(\frac{U(\ell}{\ell})^2+(\frac{U(k)}{k})^2}=9,82.10^{-5} \sqrt{(\frac{0,5}{17})^2+(\frac{0,04.10^{-6}}{1,67.10^{-6}})^2} = 3,7.10^{-6} \approx 4.10^{-6} m \) soit : \(a = 98 ± 4 μm \)

    Calculons le z-score :

    \( z = \frac{|a - a_{réf}|}{U(a)} = \frac{|100-98|}{4} = 0,5 <<2 \) c'est en accord avec la valeur de référence.

    Penser aux 3 façons: précisions, grandes valeurs et répétitions

    Il faut :

    • soit répéter l'expérience n fois et faire une moyenne, ce qui est long.
    • soit augmenter la quantité \(\ell \) en éloignant l'écran et le fil diffractant.
    • soit mesurer avec une photo par informatique : diminuer \( U(\ell) \) ce qui diminue \(U(a)\).

    Marquer comme terminé
  • 

    Pour évaluer un protocole de titrage on dose plusieurs fois une solution de concentration en masse connue \( 𝐶_E =15,0 mg/L \)

    Calculer va valeur moyenne de \(C_E\) et \(U(C_E)\) Vérifier la validité du protocole

    Calculer une valeur moyenne:

    \( \bar{C_E} = (14,2+14,7+15,2+15,9+14,7+14,1+14,9+14,4+15,1+14,6)/10 = 14,8 mg.L^{-1}\) \( U(C_E) = \frac{\sigma}{\sqrt{N}} = \frac{0,53}{\sqrt{10}} = 0,17 = 0,2 mg.L^{-1}\) soit : \(C_E = 14,8 ± 0,2 mg.L^{-1} \)

    Calculons le z-score :

    \( z = \frac{|C_E - C_{E,réf}|}{U(C_E)} = \frac{|14,8-15|}{0,2} = 1 <<2 \) c'est en accord avec la valeur de référence, le dosage est valide.

    Marquer comme terminé
• 

  Travailler avec des primitives, les exercices de mécanique

  • Révisions des règles de calcul

    

    

    

    

    

    

    

    

    

    

    

    
    

    

    

    

    

    Previous Next
  • Tennis (Réunion 2023 J1)

    
    

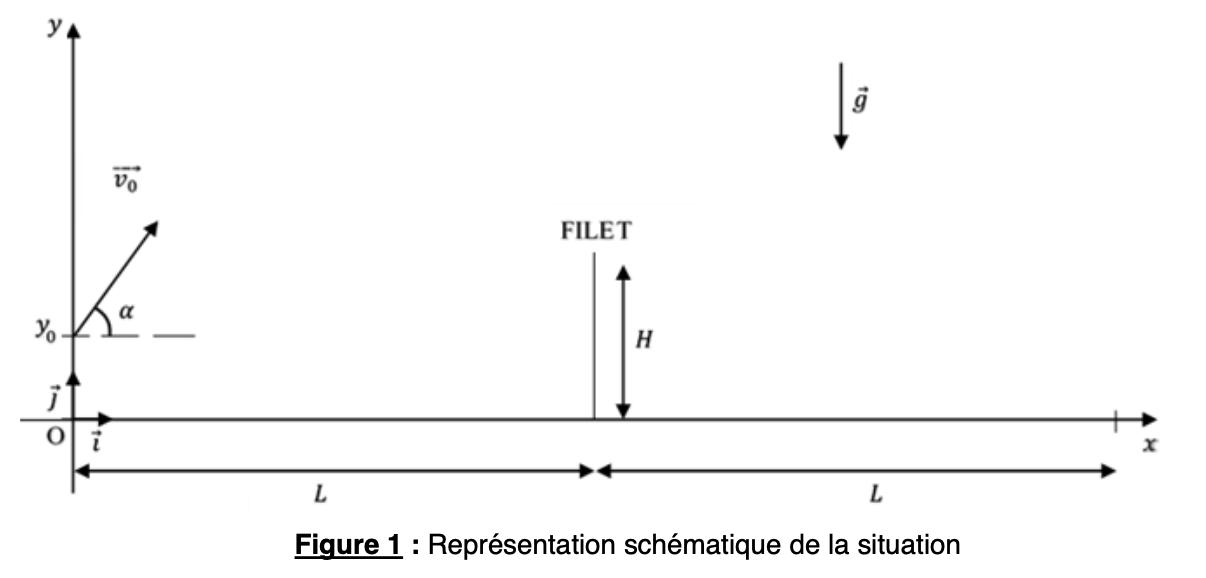
    Exprimer \(\vec{a}\) Les équations horaires Flèche Portée Trajectoire

    Référentiel : terrestre supposé Galiléen

    Système : la balle

    Bilan des forces : chute libre, il n'y a que le poids

    D'après la seconde loi de Newton :

    \(m\vec{a} = m\vec{g} \Longrightarrow \vec{a} = \vec{g} = \binom {0} {-g} \)

    Cherchons les primitives de a :

    \( \left(\begin{array} .a_x &=& \frac{dV_x}{dt} &=&0 \\ a_y &=& \frac{dV_y}{dt} &=& -g \end{array}\right) \Longrightarrow \left(\begin{array} .V_x &=&C_1 \\ V_y &=& -gt + C_2 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .V_x(0) &=& C_1 &=&V_0.cos(\alpha) \\ V_y(0) &=& -g.0 + C_2 &=& V_0.sin(\alpha) \end{array}\right) \Longrightarrow \left(\begin{array} .V_x(t) &=& \frac{dx}{dt} &=&V_0.cos(\alpha) \\ V_y(t) &=& \frac{dy}{dt} &=& -gt + V_0.sin(\alpha) \end{array}\right) \)

    Cherchons les primitives de V :

    \( \left(\begin{array} .X &=&V_0.cos(\alpha).t + C_3 \\ Y &=& \frac{-gt^2}{2} + V_0.sin(\alpha).t + C_4 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .X(0) &=& V_0.cos(\alpha).0 + C_3 &=& C_3 &=&0 \\ Y(0) &=& \frac{-g.0^2}{2} + V_0.sin(\alpha).0 + C_4 &=& C_4 &=& y_0 \end{array}\right) \Longrightarrow \left(\begin{array} .X(t) &=& V_0.cos(\alpha).t \\ Y(t) &=& \frac{-gt^2}{2} + V_0.sin(\alpha).t + y_0 \end{array}\right) \)

    Flèche = au plus haut : \( V_y=0 \)

    \( V_y(t_f) = -gt + V_0.sin(\alpha) = 0 \Longrightarrow t_f = \frac{V_0.sin(\alpha)}{g} \) \( X(t_f) = V_0.cos(\alpha).t_f = V_0.cos(\alpha) \times \frac{V_0.sin(\alpha)}{g} = \frac{V_0^2.sin(\alpha).cos(\alpha)}{g} \)

    Portée = au contact du sol : \( Y=0 \)

    \( Y(t_p) = \frac{-g}{2}\times t_p^2 + V_0.sin(\alpha).t_p + y_0 = 0 \) C'est une équation du deuxième ordre \( at_p^2 + bt_p + c = 0 \) Calculer a,b et c et utiliser la calculatrice pour obtenir les solution, la solution acceptable est celle qui donne t>0. Ensuite on peut calculer les corrdonnées X et Z avec les équations horaires en remplaçant t par sa valeur.

    Exprimer t en fonction de x :

    \( X(t) = V_0.cos(\alpha).t \Longrightarrow t = \frac{X}{V_0.cos(\alpha)} \)

    Remplacer t dans l'équation de y :

    \( Y = \frac{-g (\frac{X}{V_0.cos(\alpha)} )^2 }{2} + V_0.sin(\alpha).\frac{X}{V_0.cos(\alpha)} + y_0 \) \(\Longrightarrow Y = \frac{-g}{2.V_0^2.cos^2(\alpha)}\times X^2 + \frac{sin(\alpha)}{cos(\alpha)}\times X + y_0 \)

    Marquer comme terminé
  • Chute libre sans parachute au dessus de l'atmosphère de Felix Baumgartner (Métropole 2021 Jour 2)

    On prend pour valeur du champ de pesanteur g
    Le mouvement du centre de masse de Félix Baumgartner est étudié dans le référentiel terrestre supposé galiléen,l’axe des z est dirigé selon la verticale orientée vers le haut, l’origine O est prise au niveau du sol.
    À la date t=0s, Félix Baumgartner s’élance sans vitesse initiale d'une hauteur \( Z_{départ} \). Son mouvement est supposé vertical.⸱
    

    Exprimer \(\vec{a}\) Les équations horaires

    Référentiel : terrestre supposé Galiléen

    Système : Felix

    Bilan des forces : chute libre, il n'y a que le poids

    D'après la seconde loi de Newton :

    \(m\vec{a} = m\vec{g} \Longrightarrow \vec{a} = \vec{g} = \binom {0} {-g} \)

    Cherchons les primitives de a :

    \( \left(\begin{array} .a_x &=& \frac{dV_x}{dt} &=&0 \\ a_z &=& \frac{dV_z}{dt} &=& -g \end{array}\right) \Longrightarrow \left(\begin{array} .V_x &=&C_1 \\ V_z &=& -gt + C_2 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .V_x(0) &=& C_1 &=&0 \\ V_z(0) &=& -g.0 + C_2 &=& 0 \end{array}\right) \Longrightarrow \left(\begin{array} .V_x(t) &=& \frac{dx}{dt} &=&0 \\ V_z(t) &=& \frac{dz}{dt} &=& -gt \end{array}\right) \)

    Cherchons les primitives de V :

    \( \left(\begin{array} .X &=& C_3 \\ Z &=& \frac{-gt^2}{2} + C_4 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .X(0) &=& C_3 &=& C_3 &=&0 \\ Z(0) &=& \frac{-g.0^2}{2} + C_4 &=& C_4 &=& Z_{départ} \end{array}\right) \Longrightarrow \left(\begin{array} .X(t) &=& 0 \\ Z(t) &=& \frac{-gt^2}{2} + Z_{départ} \end{array}\right) \)

    Marquer comme terminé
  • Modélisation d’un service au tennis Nouvelle Calédonie 2022 Jour 2

    
    

    Exprimer \(\vec{a}\) Les équations horaires Portée Trajectoire

    Référentiel : terrestre supposé Galiléen

    Système : la balle

    Bilan des forces : chute libre, il n'y a que le poids

    D'après la seconde loi de Newton :

    \(m\vec{a} = m\vec{g} \Longrightarrow \vec{a} = \vec{g} = \binom {0} {-g} \)

    Cherchons les primitives de a :

    \( \left(\begin{array} .a_x &=& \frac{dV_x}{dt} &=&0 \\ a_y &=& \frac{dV_y}{dt} &=& -g \end{array}\right) \Longrightarrow \left(\begin{array} .V_x &=&C_1 \\ V_y &=& -gt + C_2 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .V_x(0) &=& C_1 &=&V_0 \\ V_y(0) &=& -g.0 + C_2 &=& 0 \end{array}\right) \Longrightarrow \left(\begin{array} .V_x(t) &=& \frac{dx}{dt} &=&V_0 \\ V_y(t) &=& \frac{dy}{dt} &=& -gt \end{array}\right) \)

    Cherchons les primitives de V :

    \( \left(\begin{array} .X &=&V_0.t + C_3 \\ Y &=& \frac{-gt^2}{2} + C_4 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .X(0) &=& V_0.0 + C_3 &=& C_3 &=&0 \\ Y(0) &=& \frac{-g.0^2}{2} + C_4 &=& C_4 &=& OB \end{array}\right) \Longrightarrow \left(\begin{array} .X(t) &=& V_0.t \\ Y(t) &=& \frac{-gt^2}{2} + OB \end{array}\right) \)

    Portée = au contact du sol : \( Y=0 \)

    \( Y(t_p) = \frac{-g}{2}\times t_p^2 + OB = 0 \) \( \frac{g}{2}\times t_p^2 = OB \) \( t_p^2 = \frac{2.OB}{g} \Longrightarrow t_p = \sqrt{\frac{2.OB}{g}} \) Ensuite on peut calculer les corrdonnées X et Y avec les équations horaires en remplaçant t par sa valeur.

    Exprimer t en fonction de x :

    \( X(t) = V_0.t \Longrightarrow t = \frac{X}{V_0} \)

    Remplacer t dans l'équation de y :

    \( Y = \frac{-g (\frac{X}{V_0} )^2 }{2} + OB \) \(\Longrightarrow Y = \frac{-g}{2.V_0^2}\times X^2 + OB \)

    Marquer comme terminé
  • Motocross Amérique du Nord 2023 J2

    

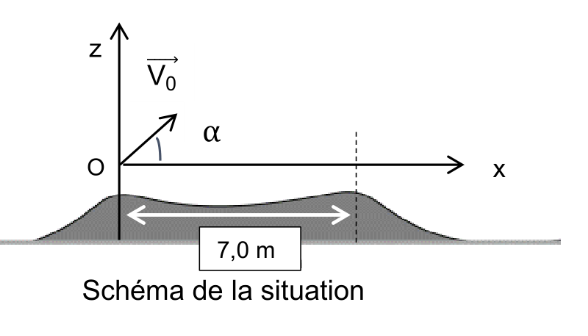
    Exprimer \(\vec{a}\) Les équations horaires Flèche Portée Trajectoire

    Référentiel : terrestre supposé Galiléen

    Système : la moto

    Bilan des forces : chute libre, il n'y a que le poids

    D'après la seconde loi de Newton :

    \(m\vec{a} = m\vec{g} \Longrightarrow \vec{a} = \vec{g} = \binom {0} {-g} \)

    Cherchons les primitives de a :

    \( \left(\begin{array} .a_x &=& \frac{dV_x}{dt} &=&0 \\ a_z &=& \frac{dV_z}{dt} &=& -g \end{array}\right) \Longrightarrow \left(\begin{array} .V_x &=&C_1 \\ V_z &=& -gt + C_2 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .V_x(0) &=& C_1 &=&V_0.cos(\alpha) \\ V_z(0) &=& -g.0 + C_2 &=& V_0.sin(\alpha) \end{array}\right) \Longrightarrow \left(\begin{array} .V_x(t) &=& \frac{dx}{dt} &=&V_0.cos(\alpha) \\ V_z(t) &=& \frac{dz}{dt} &=& -gt + V_0.sin(\alpha) \end{array}\right) \)

    Cherchons les primitives de V :

    \( \left(\begin{array} .X &=&V_0.cos(\alpha).t + C_3 \\ Z &=& \frac{-gt^2}{2} + V_0.sin(\alpha).t + C_4 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .X(0) &=& V_0.cos(\alpha).0 + C_3 &=& C_3 &=&0 \\ Z(0) &=& \frac{-g.0^2}{2} + V_0.sin(\alpha).0 + C_4 &=& C_4 &=& 0 \end{array}\right) \Longrightarrow \left(\begin{array} .X(t) &=& V_0.cos(\alpha).t \\ Z(t) &=& \frac{-gt^2}{2} + V_0.sin(\alpha).t + 0 \end{array}\right) \)

    Flèche = au plus haut : \( V_z=0 \)

    \( V_z(t_f) = -gt + V_0.sin(\alpha) = 0 \Longrightarrow t_f = \frac{V_0.sin(\alpha)}{g} \) \( X(t_f) = V_0.cos(\alpha).t_f = V_0.cos(\alpha) \times \frac{V_0.sin(\alpha)}{g} = \frac{V_0^2.sin(\alpha).cos(\alpha)}{g} \)

    Portée = au contact du sol : \( Z=0 \)

    \( Z(t_p) = \frac{-g}{2}\times t_p^2 + V_0.sin(\alpha).t_p = 0 \) \( \frac{-g}{2}\times t_p + V_0.sin(\alpha) = 0 \) \( t_p = \frac{g.V_0.sin(\alpha)}{2} \) Ensuite on peut calculer les corrdonnées X et Z avec les équations horaires en remplaçant t par sa valeur.

    Exprimer t en fonction de x :

    \( X(t) = V_0.cos(\alpha).t \Longrightarrow t = \frac{X}{V_0.cos(\alpha)} \)

    Remplacer t dans l'équation de z :

    \( Z = \frac{-g (\frac{X}{V_0.cos(\alpha)} )^2 }{2} + V_0.sin(\alpha).\frac{X}{V_0.cos(\alpha)} \) \(\Longrightarrow Z = \frac{-g}{2.V_0^2.cos^2(\alpha)}\times X^2 + \frac{sin(\alpha)}{cos(\alpha)}\times X \)

    Marquer comme terminé
  • Tir à l'arc à la perche verticale (Nouvelle Calédonie 2023 J2)

    
    

    Exprimer \(\vec{a}\) Les équations horaires Flèche Portée Trajectoire

    Référentiel : terrestre supposé Galiléen

    Système : la flèche

    Bilan des forces : chute libre, il n'y a que le poids

    D'après la seconde loi de Newton :

    \(m\vec{a} = m\vec{g} \Longrightarrow \vec{a} = \vec{g} = \binom {0} {-g} \)

    Cherchons les primitives de a :

    \( \left(\begin{array} .a_x &=& \frac{dV_x}{dt} &=&0 \\ a_y &=& \frac{dV_y}{dt} &=& -g \end{array}\right) \Longrightarrow \left(\begin{array} .V_x &=&C_1 \\ V_y &=& -gt + C_2 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .V_x(0) &=& C_1 &=&V_0.cos(\alpha) \\ V_y(0) &=& -g.0 + C_2 &=& V_0.sin(\alpha) \end{array}\right) \Longrightarrow \left(\begin{array} .V_x(t) &=& \frac{dx}{dt} &=&V_0.cos(\alpha) \\ V_y(t) &=& \frac{dy}{dt} &=& -gt + V_0.sin(\alpha) \end{array}\right) \)

    Cherchons les primitives de V :

    \( \left(\begin{array} .X &=&V_0.cos(\alpha).t + C_3 \\ Y &=& \frac{-gt^2}{2} + V_0.sin(\alpha).t + C_4 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .X(0) &=& V_0.cos(\alpha).0 + C_3 &=& C_3 &=&0 \\ Y(0) &=& \frac{-g.0^2}{2} + V_0.sin(\alpha).0 + C_4 &=& C_4 &=& h \end{array}\right) \Longrightarrow \left(\begin{array} .X(t) &=& V_0.cos(\alpha).t \\ Y(t) &=& \frac{-gt^2}{2} + V_0.sin(\alpha).t + h \end{array}\right) \)

    Flèche = au plus haut : \( V_y=0 \)

    \( V_y(t_f) = -gt + V_0.sin(\alpha) = 0 \Longrightarrow t_f = \frac{V_0.sin(\alpha)}{g} \) \( X(t_f) = V_0.cos(\alpha).t_f = V_0.cos(\alpha) \times \frac{V_0.sin(\alpha)}{g} = \frac{V_0^2.sin(\alpha).cos(\alpha)}{g} \)

    Portée = au contact du sol : \( Y=0 \)

    \( Y(t_p) = \frac{-g}{2}\times t_p^2 + V_0.sin(\alpha).t_p + h = 0 \) C'est une équation du deuxième ordre \( at_p^2 + bt_p + c = 0 \) Calculer a,b et c et utiliser la calculatrice pour obtenir les solution, la solution acceptable est celle qui donne t>0. Ensuite on peut calculer les corrdonnées X et Y avec les équations horaires en remplaçant t par sa valeur.

    Exprimer t en fonction de x :

    \( X(t) = V_0.cos(\alpha).t \Longrightarrow t = \frac{X}{V_0.cos(\alpha)} \)

    Remplacer t dans l'équation de y :

    \( Y = \frac{-g (\frac{X}{V_0.cos(\alpha)} )^2 }{2} + V_0.sin(\alpha).\frac{X}{V_0.cos(\alpha)} + h \) \(\Longrightarrow Y = \frac{-g}{2.V_0^2.cos^2(\alpha)}\times X^2 + \frac{sin(\alpha)}{cos(\alpha)}\times X + h \)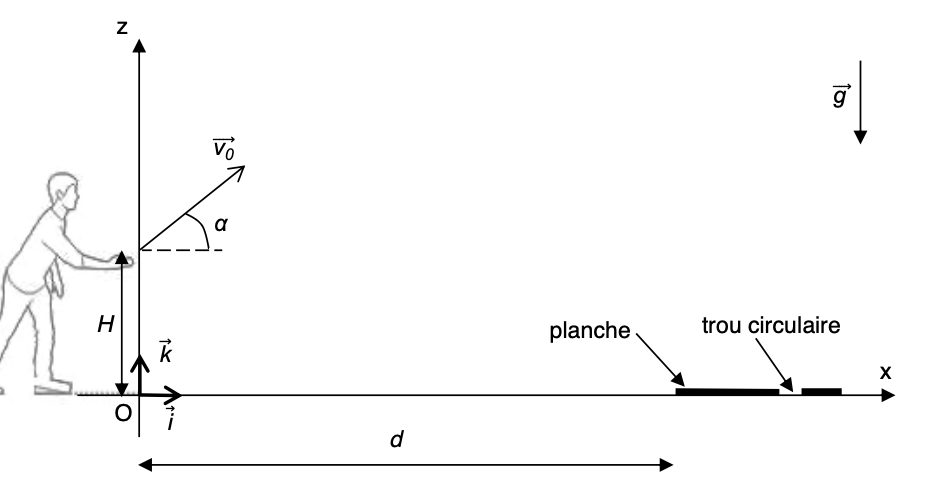

    Marquer comme terminé
  • 

    Exprimer \(\vec{a}\) Les équations horaires Flèche Portée Trajectoire

    Référentiel : terrestre supposé Galiléen

    Système : la balle

    Bilan des forces : chute libre, il n'y a que le poids

    D'après la seconde loi de Newton :

    \(m\vec{a} = m\vec{g} \Longrightarrow \vec{a} = \vec{g} = \binom {0} {-g} \)

    Cherchons les primitives de a :

    \( \left(\begin{array} .a_x &=& \frac{dV_x}{dt} &=&0 \\ a_z &=& \frac{dV_z}{dt} &=& -g \end{array}\right) \Longrightarrow \left(\begin{array} .V_x &=&C_1 \\ V_z &=& -gt + C_2 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .V_x(0) &=& C_1 &=&V_0.cos(\alpha) \\ V_z(0) &=& -g.0 + C_2 &=& V_0.sin(\alpha) \end{array}\right) \Longrightarrow \left(\begin{array} .V_x(t) &=& \frac{dx}{dt} &=&V_0.cos(\alpha) \\ V_z(t) &=& \frac{dz}{dt} &=& -gt + V_0.sin(\alpha) \end{array}\right) \)

    Cherchons les primitives de V :

    \( \left(\begin{array} .X &=&V_0.cos(\alpha).t + C_3 \\ Z &=& \frac{-gt^2}{2} + V_0.sin(\alpha).t + C_4 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .X(0) &=& V_0.cos(\alpha).0 + C_3 &=& C_3 &=&0 \\ Z(0) &=& \frac{-g.0^2}{2} + V_0.sin(\alpha).0 + C_4 &=& C_4 &=& H \end{array}\right) \Longrightarrow \left(\begin{array} .X(t) &=& V_0.cos(\alpha).t \\ Z(t) &=& \frac{-gt^2}{2} + V_0.sin(\alpha).t + H \end{array}\right) \)

    Flèche = au plus haut : \( V_z=0 \)

    \( V_z(t_f) = -gt + V_0.sin(\alpha) = 0 \Longrightarrow t_f = \frac{V_0.sin(\alpha)}{g} \) \( X(t_f) = V_0.cos(\alpha).t_f = V_0.cos(\alpha) \times \frac{V_0.sin(\alpha)}{g} = \frac{V_0^2.sin(\alpha).cos(\alpha)}{g} \)

    Portée = au contact du sol : \( Z=0 \)

    \( Z(t_p) = \frac{-g}{2}\times t_p^2 + V_0.sin(\alpha).t_p + H = 0 \) C'est une équation du deuxième ordre \( at_p^2 + bt_p + c = 0 \) Calculer a,b et c et utiliser la calculatrice pour obtenir les solution, la solution acceptable est celle qui donne t>0. Ensuite on peut calculer les corrdonnées X et Z avec les équations horaires en remplaçant t par sa valeur.

    Exprimer t en fonction de x :

    \( X(t) = V_0.cos(\alpha).t \Longrightarrow t = \frac{X}{V_0.cos(\alpha)} \)

    Remplacer t dans l'équation de z :

    \( Z = \frac{-g (\frac{X}{V_0.cos(\alpha)} )^2 }{2} + V_0.sin(\alpha).\frac{X}{V_0.cos(\alpha)} + H \) \(\Longrightarrow Z = \frac{-g}{2.V_0^2.cos^2(\alpha)}\times X^2 + \frac{sin(\alpha)}{cos(\alpha)}\times X + H \)

    Marquer comme terminé
  • Le scanner à rayons X (Réunion SI 2023 Jour 1)

    
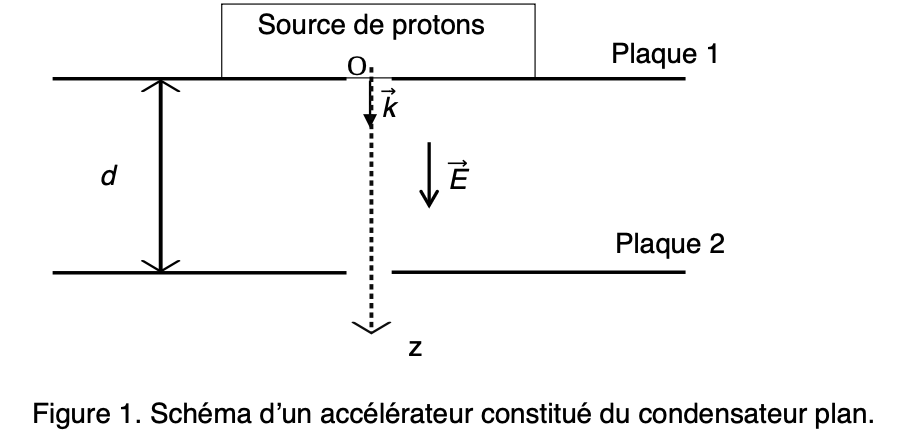
    Un proton de masse m et de charge positive q = +e est libéré en O sans vitesse initiale  Le poids est négligeable.

    Exprimer \(\vec{a}\) Les équations horaires temps et vitesse à l'arrivée sur l'anode

    Référentiel : terrestre supposé Galiléen

    Système : le proton

    Bilan des forces : Force électrique sur le proton

    D'après la seconde loi de Newton :

    \(m\vec{a} = q.\vec{E} \Longrightarrow \vec{a} = \frac{+e}{m}\times \vec{E} = \binom {0} {\frac{eE}{m}}\)

    Cherchons les primitives de a : Un seul axe, une seule coordonnée suffit

    \( a_z = \frac{dV_z}{dt} = \frac{eE}{m} \Longrightarrow V_z = \frac{eE}{m} \times t + C_1 \) or à t = 0 on a les conditions initiales : \( V_z(0) =\frac{eE}{m} \times 0 + C_1 = 0 \Longrightarrow V_z(t) = \frac{dz}{dt} =\frac{eE}{m} \times t \)

    Cherchons les primitives de V :

    \( z = \frac{eE}{2.m} \times t^2 + C_3 \) or à t = 0 on a les conditions initiales : \( z(0) = \frac{eE}{2.m} \times 0^2 + C_3 = C_3 = 0 \Longrightarrow z(t) = \frac{eE}{2.m} \times t^2 \)

    temps et vitesse à l'arrivée sur l'anode

    Calcul du temps t pour z = d: \( Z(t_s) = d = \frac{eE}{2.m} \times t_s^2 \Longrightarrow t_s^2 = \frac{2.m.d}{e.E} \Longrightarrow t_s = \sqrt{\frac{2.m.d}{e.E}} \) \( V_z(t_s) = \frac{eE}{m} \times t_s = \frac{eE}{m} \times \sqrt{\frac{2.m.d}{e.E}} \) \( V_z(t_s) = \sqrt{ (\frac{eE}{m})^2} \times \sqrt{\frac{2.m.d}{e.E}}= \sqrt{\frac{2.m.de^2E^2}{e.E.m^2}} = \sqrt{\frac{2.d.e.E}{m}} \)

    Marquer comme terminé
  • Le scanner à rayons X (Réunion SI 2023 Jour 1)

    
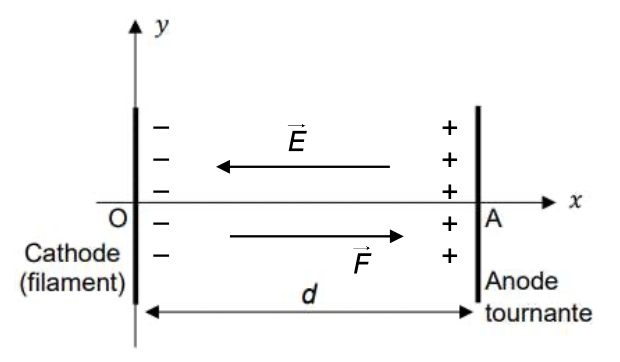
    Un électron de masse m et de charge négative q = -e est libéré en O sans vitesse initiale  Le poids est négligeable.

    Exprimer \(\vec{a}\) Les équations horaires temps et vitesse à l'arrivée sur l'anode

    Référentiel : terrestre supposé Galiléen

    Système : l'électron

    Bilan des forces : Force électrique sur l'électron

    D'après la seconde loi de Newton :

    \(m\vec{a} = q.\vec{E} \Longrightarrow \vec{a} = \frac{-e}{m}\times \vec{E} = \binom {\frac{eE}{m}}{0} \)

    Cherchons les primitives de a :

    \( \left(\begin{array} .a_x &=& \frac{dV_x}{dt} &=&\frac{eE}{m} \\ a_y &=& \frac{dV_y}{d} &=& 0\end{array}\right) \Longrightarrow \left(\begin{array} .V_x &=&\frac{eE}{m} \times t + C_1 \\ V_y &=& C_2 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .V_x(0) &=&\frac{eE}{m} \times 0 + C_1 &=&0 \\ V_y(0) &=& C_2 &=& 0 \end{array}\right) \Longrightarrow \left(\begin{array} .V_x(t) &=& \frac{dx}{dt} &=&\frac{eE}{m} \times t \\ V_y(t) &=& \frac{dy}{dt} &=& 0 \end{array}\right) \)

    Cherchons les primitives de V :

    \( \left(\begin{array} .X &=&\frac{eE}{2.m} \times t^2 + C_3 \\ Y &=& C_4 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .X(0) &=& \frac{eE}{2.m} \times 0^2 + C_3 &=& C_3 &=&0 \\ Y(0) &=& C_4 &=& 0 \end{array}\right) \Longrightarrow \left(\begin{array} .X(t) &=& \frac{eE}{2.m} \times t^2 \\ Y(t) &=& 0 \end{array}\right) \)

    temps et vitesse à l'arrivée sur l'anode

    Calcul du temps t pour x = d: \( X(t_s) = d = \frac{eE}{2.m} \times t_s^2 \Longrightarrow t_s^2 = \frac{2.m.d}{e.E} \Longrightarrow t_s = \sqrt{\frac{2.m.d}{e.E}} \) \( V_x(t_s) = \frac{eE}{m} \times t_s = \frac{eE}{m} \times \sqrt{\frac{2.m.d}{e.E}} \) \( V_x(t_s) = \sqrt{ (\frac{eE}{m})^2} \times \sqrt{\frac{2.m.d}{e.E}}= \sqrt{\frac{2.m.de^2E^2}{e.E.m^2}} = \sqrt{\frac{2.d.e.E}{m}} \)

    Marquer comme terminé
  • Imprimante à jet d'encre continu (Métropole septembre 2023 Jour 2)

    
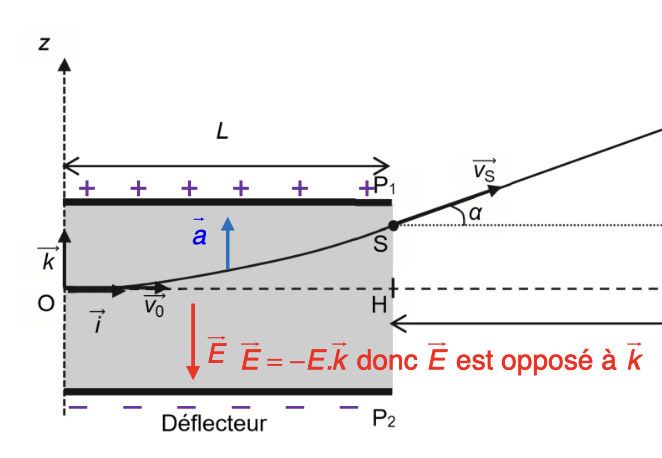
    masse d’une goutte d’encre : m charge électrique d’une goutte : q = \(–4×10^{–13}\)C Le poids est négligeable.

    Exprimer \(\vec{a}\) Les équations horaires \(tan(\alpha)\) Trajectoire

    Référentiel : terrestre supposé Galiléen

    Système : la goute d'encre chargée

    Bilan des forces : Force électrique sur la goute chargée

    D'après la seconde loi de Newton :

    \(m\vec{a} = q.\vec{E} \Longrightarrow \vec{a} = \frac{q}{m}\times \vec{E} = \binom {0} {\frac{-qE}{m}} \)

    Cherchons les primitives de a :

    \( \left(\begin{array} .a_x &=& \frac{dV_x}{dt} &=&0 \\ a_z &=& \frac{dV_z}{dt} &=& \frac{-qE}{m} \end{array}\right) \Longrightarrow \left(\begin{array} .V_x &=&C_1 \\ V_z &=& \frac{-qE}{m} t + C_2 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .V_x(0) &=& C_1 &=&V_0 \\ V_z(0) &=& \frac{-qE}{m} .0 + C_2 &=& 0 \end{array}\right) \Longrightarrow \left(\begin{array} .V_x(t) &=& \frac{dx}{dt} &=&V_0 \\ V_z(t) &=& \frac{dz}{dt} &=& \frac{-qE}{m} t \end{array}\right) \)

    Cherchons les primitives de V :

    \( \left(\begin{array} .X &=&V_0.t + C_3 \\ Z &=& \frac{-qE}{2m}t^2 + C_4 \end{array}\right) \) or à t = 0 on a les conditions initiales \( \left(\begin{array} .X(0) &=& V_0.0 + C_3 &=& C_3 &=&0 \\ Z(0) &=& \frac{-qE}{2m}.0^2 + C_4 &=& C_4 &=& 0 \end{array}\right) \Longrightarrow \left(\begin{array} .X(t) &=& V_0.t \\ Z(t) &=& \frac{-qE}{2m}.t^2 \end{array}\right) \)

    \(tan(\alpha) = \frac{opposé}{adjacent}\) pour x = L

    Calcul de t à la sortie où x = L: \( X(t_s) = L = V_0.t_s \Longrightarrow t_s = \frac{L}{V_0} \) \( tan(\alpha) = \frac{opposé}{adjacent} = \frac{V_z(t_s)}{V_x(t_s)}\) \( V_x(t_s) = V_0 \) \( V_z(t_s) = \frac{-qE}{m}\times t_s = \frac{-qE}{m}\times \frac{L}{V_0} = \frac{-q.E.L}{m.V_0}\) \( tan(\alpha) = \frac{V_z(t_s)}{V_x(t_s)} = \frac{\frac{-q.E.L}{m.V_0}}{V_0} =\frac{-q.E.L}{m.V_0^2} \)

    Exprimer t en fonction de x :

    \( X(t) = V_0.t \Longrightarrow t = \frac{X}{V_0} \)

    Remplacer t dans l'équation de z :

    \( Z = \frac{-qE}{2m} \times (\frac{X}{V_0})^2 \Longrightarrow Z = \frac{-qEX^2}{2m.V_0^2} \)

    Marquer comme terminé
  • A la découverte de Saturne (Métropole 2023 J1)

    
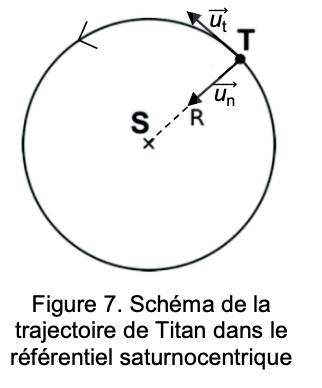
    Titan de masse m est un satellite de Saturne de masse Ms

    Exprimer \(\vec{a}\) vitesse V Période T 3eme loi de Kepler

    Référentiel : saturnocentrique supposé Galiléen

    Système : Titan

    Bilan des forces : Force de gravitation

    D'après la seconde loi de Newton :

    \(m\vec{a} = m\vec{F_g}= \frac{G.m.Ms}{R^2} \vec{U_N}\Longrightarrow \vec{a} = \binom {0} {\frac{G.Ms}{R^2}} \) Dans le repère de Frénet : \( \vec{a}= \frac{dv}{dt} \vec{U_T} + \frac{v^2}{R} \vec{U_N} =\binom {\frac{dv}{dt}} {\frac{v^2}{R} } \)

    Dans le repère de Frénet :

    \( \frac{dv}{dt} = 0 \Longrightarrow v = constante \) \( \frac{v^2}{R} = \frac{G.Ms}{R^2} \Longrightarrow v^2 = \frac{G.Ms}{R} \) Pourune trajectoire circulaire la vitesse est uniforme et vaut : \( v = \sqrt{\frac{G.Ms}{R}} \)

    la vitesse est uniforme donc sur un tour complet \( v = \frac{d_{1 tour}}{t_{1 tour}}=\frac{2\pi R}{T} \)

    \( v^2 = \frac{4.\pi^2 R^2}{T^2} = (\sqrt{\frac{G.Ms}{R}})^2 = \frac{G.Ms}{R} \) \( \frac{4.\pi^2 R^2}{T^2} = \frac{G.Ms}{R} \Longrightarrow \frac{4.\pi^2 R^2.R}{G.Ms} = T^2 \) \( T = \sqrt{\frac{4.\pi^2 R^3}{G.Ms}} \)

    La troisième loi de Kepler dit :

    \( \frac{T^2}{R^3} = constante \) Or \( T = \sqrt{\frac{4.\pi^2 R^3}{G.Ms}} \Longrightarrow T^2 = \frac{4.\pi^2 R^3}{G.Ms} \) Soit : \( \frac{T^2 }{R^3} = \frac{4.\pi^2}{G.Ms} \)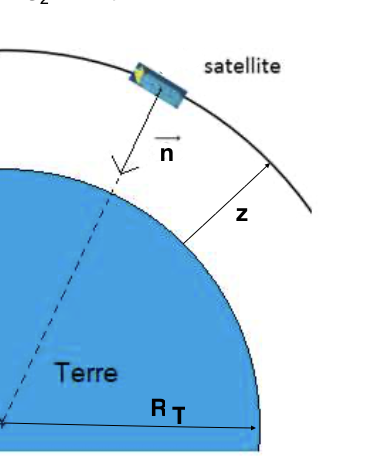

    Marquer comme terminé
  • 
    

    
    Soit un satellite de masse m  de la Terre de masse Mt à une altitude z.

    Exprimer \(\vec{a}\) vitesse V Période T 3eme loi de Kepler Altitude d'un satellite géostationnaire

    Référentiel : Géocentrique supposé Galiléen

    Système : Le satellite

    Bilan des forces : Force de gravitation

    D'après la seconde loi de Newton :

    \(m\vec{a} = m\vec{F_g}= \frac{G.m.Mt}{(R_T+z)^2} \vec{n}\Longrightarrow \vec{a} = \binom {0} {\frac{G.Mt}{(R_T+z)^2}} \) Dans le repère de Frénet : \( \vec{a}= \frac{dv}{dt} \vec{\tau} + \frac{v^2}{(R_T+z)} \vec{n} =\binom {\frac{dv}{dt}} {\frac{v^2}{(R_T+z)} } \)

    Dans le repère de Frénet :

    \( \frac{dv}{dt} = 0 \Longrightarrow v = constante \) \( \frac{v^2}{(R_T+z)} = \frac{G.Mt}{(R_T+z)^2} \Longrightarrow v^2 = \frac{G.Mt}{(R_T+z)} \) Pourune trajectoire circulaire la vitesse est uniforme et vaut : \( v = \sqrt{\frac{G.Mt}{(R_T+z)}} \)

    la vitesse est uniforme donc sur un tour complet \( v = \frac{d_{1 tour}}{t_{1 tour}}=\frac{2\pi (R_T+z)}{T} \)

    \( v^2 = \frac{4.\pi^2 (R_T+z)^2}{T^2} = (\sqrt{\frac{G.Mt}{(R_T+z)}})^2 = \frac{G.Mt}{(R_T+z)} \) \( \frac{4.\pi^2 (R_T+z)^2}{T^2} = \frac{G.Mt}{(R_T+z)} \Longrightarrow \frac{4.\pi^2 (R_T+z)^2.(R_T+z)}{G.Mt} = T^2 \) \( T = \sqrt{\frac{4.\pi^2 (R_T+z)^3}{G.Mt}} \)

    La troisième loi de Kepler dit :

    \( \frac{T^2}{(R_T+z)^3} = constante \) Or \( T = \sqrt{\frac{4.\pi^2 (R_T+z)^3}{G.Mt}} \Longrightarrow T^2 = \frac{4.\pi^2 (R_T+z)^3}{G.Mt} \) Soit : \( \frac{T^2 }{(R_T+z)^3} = \frac{4.\pi^2}{G.Mt} \)

    satellite géostationnaire = reste au dessus du même point donc : T = 24h :

     \( T = \sqrt{\frac{4.\pi^2 (R_T+z)^3}{G.Mt}} \Longrightarrow T^2 = \frac{4.\pi^2 (R_T+z)^3}{G.Mt} \) Soit : \( (R_T+z)^3 = \frac{G.Mt.T^2 }{4.\pi^2} \) On prend la racine cubique : Soit : \( (R_T+z) = \sqrt[3]{\frac{G.Mt.T^2 }{4.\pi^2}} \)

    Marquer comme terminé
• 

  Travailler avec des équations compliquées, bilan d'énergie ...

  • Révisions des règles de calcul

    

    

    

    

    
    

    

    

    

    

    

    

    
    

    Previous Next
  • Conservation de l'énergie mécanique : \( \frac{1}{2}mv_i^2 + mgz_i = \frac{1}{2}mv_f^2 + mgz_f \)

    Exprimer \(v_i\) Exprimer \(v_f\) Exprimer \(z_f\) Exprimer \(z_i\)

    Diviser par m pour simplifier : \( \frac{1}{2}v_i^2 + gz_i = \frac{1}{2}v_f^2 + gz_f \) Isoler le bon terme : \( \frac{1}{2}v_i^2 = \frac{1}{2}v_f^2 + gz_f - gz_i \) Multiplier par 2 : \( v_i^2 = v_f^2 + 2gz_f - 2gz_i \) Prendre la racine de l'égalité : \( v_i = \sqrt{v_f^2 + 2gz_f - 2gz_i}=\sqrt{v_f^2 + 2g(z_f -z_i)} \)

    Diviser par m pour simplifier : \( \frac{1}{2}v_i^2 + gz_i = \frac{1}{2}v_f^2 + gz_f \) Isoler le bon terme : \( \frac{1}{2}v_f^2 = \frac{1}{2}v_i^2 + gz_i - gz_f\) Multiplier par 2 : \( v_f^2 = v_i^2 + 2gz_i - 2gz_f\) Prendre la racine de l'égalité : \( v_f = \sqrt{v_i^2 + 2gz_i - 2gz_f}=\sqrt{v_i^2 + 2g(z_i -z_f)}\)

    Diviser par m pour simplifier : \( \frac{1}{2}v_i^2 + gz_i = \frac{1}{2}v_f^2 + gz_f \) Isoler le bon terme : \( gz_f = \frac{1}{2}v_i^2 + gz_i - \frac{1}{2}v_f^2 = \frac{1}{2}(v_i^2 - v_f^2) + gz_i \) Diviser par g : \( z_f = \frac{1}{2g}(v_i^2 - v_f^2) + z_i \)

    Diviser par m pour simplifier : \( \frac{1}{2}v_i^2 + gz_i = \frac{1}{2}v_f^2 + gz_f \) Isoler le bon terme : \( gz_i = \frac{1}{2}v_f^2 + gz_f - \frac{1}{2}v_i^2 = \frac{1}{2}(v_f^2 - v_i^2) + gz_f \) Diviser par g : \( z_i = \frac{1}{2g}(v_f^2 - v_i^2) + z_f \)

    Marquer comme terminé
  • Théorème de l'énergie cinétique pour une charge dans un champs E qui parcours une ditance d dans le sens du champ : \( \frac{1}{2}mv_f^2 - \frac{1}{2}mv_i^2 = W_d(\vec{F_E}) = q.d.E \)

    Exprimer \(v_i\) Exprimer \(v_f\) Exprimer \(E\)

    Diviser par m/2 : \( v_f^2 - v_i^2 = \frac{2.q.d.E}{m} \) Isoler le bon terme : \( v_f^2 - \frac{2.q.d.E}{m} = v_i^2\) Prendre la racine de l'égalité : \( v_i = \sqrt{v_f^2 - \frac{2.q.d.E}{m}} \)

    Diviser par m/2 : \( v_f^2 - v_i^2 = \frac{2.q.d.E}{m} \) Isoler le bon terme : \( v_f^2 = v_i^2 + \frac{2.q.d.E}{m}\) Prendre la racine de l'égalité : \( v_f = \sqrt{v_i^2 + \frac{2.q.d.E}{m}} \)

    Diviser par m/2 : \( v_f^2 - v_i^2 = \frac{2.q.d.E}{m} \) Isoler le bon terme : \( (v_f^2 - v_i^2 ) = \frac{2.q.d.E}{m}\) Isoler E en passant les autres facteurs de l'autre côté : \( \frac{m}{2.q.d}(v_f^2 - v_i^2 ) = E \)

    Marquer comme terminé
  • La relation de Bernouilli en mécanique des fluides : \( \frac{1}{2}\rho v_i^2 + \rho gz_i + P_i= \frac{1}{2}\rho v_f^2 + \rho gz_f +P_f\)

    Exprimer \(P_i\) Exprimer \(v_i\) Exprimer \(v_f\) Exprimer \(z_f\) Exprimer \(z_i\)

    \( \frac{1}{2}\rho v_i^2 + \rho gz_i + P_i= \frac{1}{2}\rho v_f^2 + \rho gz_f +P_f\) Isoler le bon terme : \( \frac{1}{2}\rho v_i^2 + \rho gz_i + P_i - \frac{1}{2}\rho v_f^2 - \rho gz_f = P_f \) Factoriser : \( P_f = \frac{1}{2}\rho (v_i^2 - v_f^2)+ \rho g(z_i - z_f) + P_i \)

    \( \frac{1}{2}\rho v_i^2 + \rho gz_i + P_i= \frac{1}{2}\rho v_f^2 + \rho gz_f +P_f\) Isoler le bon terme : \( \frac{1}{2}\rho v_i^2 = \frac{1}{2}\rho v_f^2 + \rho gz_f - \rho gz_i + P_f - P_i \) \( Multiplier\ par\ 2\ et\ diviser\ par \ \rho \ : \ v_i^2 = v_f^2 + 2.g.(z_f - z_i) + \frac{2}{\rho}.(P_f - P_i) \) Prendre la racine de l'égalité : \( v_i = \sqrt{v_f^2 + 2.g.(z_f - z_i) + \frac{2}{\rho}.(P_f - P_i)} \)

    \( \frac{1}{2}\rho v_i^2 + \rho gz_i + P_i= \frac{1}{2}\rho v_f^2 + \rho gz_f +P_f\) Isoler le bon terme : \( \frac{1}{2}\rho v_f^2 = \frac{1}{2}\rho v_i^2 + \rho gz_i + P_i - \rho gz_f - P_f \) \( Multiplier\ par\ 2\ et\ diviser\ par \ \rho \ : \ v_f^2 = v_i^2 + 2.g.(z_i - z_f) + \frac{2}{\rho}.(P_i - P_f) \) Prendre la racine de l'égalité : \( v_f = \sqrt{v_i^2 + 2.g.(z_i - z_f) + \frac{2}{\rho}.(P_i - P_f)} \)

    \( \frac{1}{2}\rho v_i^2 + \rho gz_i + P_i= \frac{1}{2}\rho v_f^2 + \rho gz_f +P_f\) Isoler le bon terme : \( \rho gz_i = \frac{1}{2}\rho v_f^2 - \frac{1}{2}\rho v_i^2 + \rho gz_f + P_f - P_i \) \(Diviser\ par\ \rho g\ :\ z_i = \frac{1}{2g} (v_f^2 - v_i^2) + z_f + \frac{P_f - P_i}{\rho g} \)

    \( \frac{1}{2}\rho v_i^2 + \rho gz_i + P_i= \frac{1}{2}\rho v_f^2 + \rho gz_f +P_f\) Isoler le bon terme : \( \rho gz_f = \frac{1}{2}\rho v_i^2 - \frac{1}{2}\rho v_f^2 + \rho gz_i + P_i - P_f \) \(Diviser\ par\ \rho g\ :\ z_f = \frac{1}{2g} (v_i^2 - v_f^2) + z_i + \frac{P_i - P_f}{\rho g} \)

    Marquer comme terminé
• 

  Travailler avec des équations différentielles : condensateur, thermodynamique, cinétique...

  • Révisions des règles de calcul

    
    

    

    

    

    

    

    

    

    

    

    

    
    

    
    

    

    Previous Next
  • L'activité correspond au nombre de désintégration par seconde et est propportionnel au nombre de noyau : \( A = -\frac{dN}{dt} = \lambda \times N \)
    pour t=0 : il y a \( N_0 \) noyaux

    Proposer une solution N(t) = ... Vérifier la solution Trouver l'expression t=f(N,N_0,\lambda)

    Savoir mathématique: les équations du premier ordre : y'= ay + b on pour solution : \( y(t) = C_1.e^{a \times t} - \frac{b}{a} \)

    Identifions :

    \( A = -\frac{dN}{dt} = \lambda \times N \Longrightarrow \frac{dN}{dt} = - \lambda \times N \) donc \( a = - \lambda \ et \ b = 0 \Longrightarrow y(t) = N(t) = C_1.e^{- \lambda \times t} - 0 \)

    Utilisons la condition initiale \( N(0) = N_0 \) : \( N(0) = C_1.e^{- \lambda \times 0} = C_1 = N_0 \)

    \( N(t) = N_0.e^{- \lambda \times t} \)

    Cherchons la dérivée de N(t)

    \( N(t) = N_0.e^{- \lambda \times t} \Longrightarrow \left\{\begin{array}. \frac{dN}{dt} = - \lambda \times N_0.e^{- \lambda \times t} \\ - \lambda \times N = - \lambda \times N_0.e^{- \lambda \times t} \end{array} \right. \) donc on a bien :

    \( \frac{dN}{dt} = - \lambda \times N \)

    \( N(t) = N_0.e^{- \lambda \times t} \)

    On isole la fonction exponentielle :

    \( \frac{N(t)}{N_0} = e^{- \lambda \times t} \)

    On applique la fonction ln :

    \( ln( \frac{N(t)}{N_0} ) = - \lambda \times t \)

    On réorganise les facteurs :

    \( \frac{-1}{\lambda} \times ln( \frac{N(t)}{N_0} ) = t \)

    \( t = \frac{-1}{\lambda} \times ln( \frac{N_0}{N(t)} ) \)

    Marquer comme terminé
  • Une cinétique du premier ordre suit la loi suivante ou [R] représente la concentration d'un réactif : \(v= -\frac{d[R]}{dt} = k \times [R] \)
    pour t=0 : la concentration initiale vaut \( [R]_0 \)

    Proposer une solution [R](t) = ... Vérifier la solution Trouver l'expression t=f([R],[R]_0,\lambda)

    Savoir mathématique: les équations du premier ordre : y'= ay + b on pour solution : \( y(t) = C_1.e^{a \times t} - \frac{b}{a} \)

    Identifions :

    \( -\frac{d[R]}{dt} = k \times [R] \Longrightarrow \frac{d[R]}{dt} = - k \times [R] \) donc \( a = - k \ et \ b = 0 \Longrightarrow y(t) = [R](t) = C_1.e^{- k \times t} - 0 \)

    Utilisons la condition initiale \( [R](0) = [R]_0 \) : \( N(0) = C_1.e^{- k \times 0} = C_1 = [R]_0 \)

    \( [R](t) = [R]_0.e^{- k \times t} \)

    Cherchons la dérivée de N(t)

    \( [R](t) = [R]_0.e^{- k \times t} \Longrightarrow \left\{\begin{array} . \frac{d[R]}{dt} = - k \times [R]_0.e^{- k \times t} \\ - k \times [R] = - k \times [R]_0.e^{- k \times t} \end{array} \right. \) donc on a bien :

    \( \frac{d[R]}{dt} = - k \times [R] \)

    \( [R](t) = [R]_0.e^{- k \times t} \)

    On isole la fonction exponentielle :

    \( \frac{[R](t)}{[R]_0} = e^{- k \times t} \)

    On applique la fonction ln :

    \( ln( \frac{[R](t)}{[R]_0} ) = - k \times t \)

    On réorganise les facteurs :

    \( \frac{-1}{k} \times ln( \frac{[R](t)}{[R]_0} ) = t \)

    \( t = \frac{-1}{k} \times ln( \frac{[R]_0}{[R](t)} ) \)

    Marquer comme terminé
  • Lors de la décharge d'un condensateur on obtient l'équation suivante : \( Uc + R.C.\frac{Uc}{dt} = 0 \)
    pour t=0 : la tension initiale vaut \( U_0 \)

    Proposer une solution Uc(t) = ... Vérifier la solution Trouver l'expression t=f(Uc,U_0,\lambda)

    Savoir mathématique: les équations du premier ordre : y'= ay + b on pour solution : \( y(t) = C_1.e^{a \times t} - \frac{b}{a} \)

    Identifions :

    \( R.C.\frac{dUc}{dt} = -Uc \Longrightarrow \frac{dUc}{dt} = \frac{-1}{R.C}.Uc \) donc \( a = \frac{-1}{R.C} \ et \ b = 0 \Longrightarrow y(t) = Uc(t) = C_1.e^{\frac{-t}{R.C}} - 0 \)

    Utilisons la condition initiale \( Uc(0) = U_0 \) : \( N(0) = C_1.e^{\frac{-0}{R.C}} = C_1 = U_0 \)

    \( Uc(t) = U_0.e^{\frac{-t}{R.C}} \)

    Cherchons la dérivée de N(t)

    \( Uc(t) = U_0.e^{\frac{-t}{R.C}} \Longrightarrow \left\{\begin{array} .\frac{dUc}{dt} = \frac{-1}{R.C} \times U_0.e^{\frac{-t}{R.C}} \\ \frac{-1}{R.C} \times Uc = \frac{-1}{R.C} \times U_0.e^{\frac{-t}{R.C}} \end{array} \right. \) donc on a bien :

    \( \frac{dUc}{dt} = \frac{-1}{R.C} \times Uc \)

    \( Uc(t) = U_0.e^{\frac{-t}{R.C}} \)

    On isole la fonction exponentielle :

    \( \frac{Uc(t)}{U_0} = e^{\frac{-t}{R.C}} \)

    On applique la fonction ln :

    \( ln( \frac{Uc(t)}{U_0} ) = \frac{-t}{R.C} \)

    On réorganise les facteurs :

    \( -RC \times ln( \frac{Uc(t)}{U_0} ) = t \)

    \( t = -RC \times ln( \frac{Uc(t)}{U_0} ) \)

    Marquer comme terminé
  • Lors de la charge d'un condensateur on obtient l'équation suivante : \( Uc + R.C.\frac{Uc}{dt} = E \)
    pour t=0 : la tension initiale vaut \( 0 \)

    Proposer une solution Uc(t) = ... Vérifier la solution Trouver l'expression t=f(Uc,U_0,\lambda)

    Savoir mathématique: les équations du premier ordre : y'= ay + b on pour solution : \( y(t) = C_1.e^{a \times t} - \frac{b}{a} \)

    Identifions :

    \( R.C.\frac{dUc}{dt} = E - Uc \Longrightarrow \frac{dUc}{dt} = \frac{E}{R.C} + \frac{-1}{R.C}.Uc \) donc \( a = \frac{-1}{R.C} \ et \ b = \frac{E}{R.C} \Longrightarrow y(t) = Uc(t) = C_1.e^{\frac{-t}{R.C}} + E \)

    Utilisons la condition initiale \( Uc(0) = U_0 \) : \( N(0) = C_1.e^{\frac{-0}{R.C}} + E = C_1 + E = 0 \Longrightarrow C_1 = - E\)

    \( Uc(t) = E -E.e^{\frac{-t}{R.C}} = E.(1 - e^{\frac{-t}{R.C}}) \)

    Cherchons la dérivée de N(t)

    \( Uc = E.(1 - e^{\frac{-t}{R.C}}) \Longrightarrow \left\{\begin{array} .R.C.\frac{dUc}{dt} = \frac{RC}{R.C} \times E.e^{\frac{-t}{R.C}} = E.e^{\frac{-t}{R.C}} \\ E - Uc = E - E.(1 - e^{\frac{-t}{R.C}}) = E.e^{\frac{-t}{R.C}} \end{array} \right. \) donc on a bien :

    \( \frac{dUc}{dt} = \frac{-1}{R.C} \times Uc \)

    \( Uc(t) = E.(1 - e^{\frac{-t}{R.C}}) \)

    On isole la fonction exponentielle :

    \( \frac{Uc(t)}{E} = 1 - e^{\frac{-t}{R.C}} \Longrightarrow e^{\frac{-t}{R.C}} = 1 - \frac{Uc(t)}{E}\)

    On applique la fonction ln :

    \( \frac{-t}{R.C} = ln( 1 - \frac{Uc(t)}{E}) \)

    On réorganise les facteurs :

    \( t = -RC \times ln( 1 - \frac{Uc(t)}{E}) \)

    \( t = -RC \times ln( 1 - \frac{Uc(t)}{E}) \)

    Marquer comme terminé
  • Lors de la perte de chaleur à travers une paroie on obtient l'équation suivante pour la température T : \( \frac{dT}{dt} = \frac{-h.S}{m.c}T + \frac{h.S}{m.c} T_{ext} \)
    pour t=0 : la température initiale vaut \(T_{init} \)

    Proposer une solution T(t) = ... Vérifier la solution

    Savoir mathématique: les équations du premier ordre : y'= ay + b on pour solution : \( y(t) = C_1.e^{a \times t} - \frac{b}{a} \)

    Identifions :

    \( \frac{dT}{dt} = \frac{-h.S}{m.c}T + \frac{h.S}{m.c} T_{ext} \) donc \( a = \frac{-h.S}{m.c} \ et \ b = \frac{h.S}{m.c} T_{ext} \Longrightarrow y(t) = T(t) = C_1.e^{\frac{-h.S.t}{m.c}} + T_{ext} \)

    Utilisons la condition initiale \( T(0) = T_{init} \) : \( T(0) = C_1.e^{\frac{-h.S.0}{m.c}} + T_{ext} = C_1 + T_{ext} = T_{init} \Longrightarrow C_1 = T_{init} - T_{ext} \)

    \( T(t) = (T_{init} - T_{ext}).e^{\frac{-h.S.t}{m.c}} + T_{ext} \)

    \( T(t) = (T_{init} - T_{ext}).e^{\frac{-h.S.t}{m.c}} + T_{ext} \)

    Cherchons la dérivée de T(t)

    \(\frac{dT}{dt} = \frac{-h.S}{m.c}.(T_{init} - T_{ext}).e^{\frac{-h.S.t}{m.c}} \) \(\frac{-h.S}{m.c}.T + \frac{h.S}{m.c}.T_{ext} = \frac{-h.S}{m.c}.((T_{init} - T_{ext}).e^{\frac{-h.S.t}{m.c}} + T_{ext}) + \frac{-h.S}{m.c} \times (-T_{ext}) = \frac{-h.S}{m.c}.(T_{init} - T_{ext}).e^{\frac{-h.S.t}{m.c}} \) donc on a bien :

    \( \frac{dT}{dt} = \frac{-h.S}{m.c}.T + \frac{h.S}{m.c}.T_{ext} \)

    Marquer comme terminé
  • Exercice : Étude approfondie du mouvement d’un projectile

    Énoncé :

    Un footballeur tire un ballon sous un angle de 30° par rapport à l’horizontale avec une vitesse initiale de 25 m/s. On néglige la résistance de l’air et on considère que l’accélération de la pesanteur est g = 9,81 m/s². Le but de cet exercice est d’étudier en détail le mouvement du ballon à différentes étapes et d’en extraire des conclusions physiques pertinentes.

    1. Décomposer la vitesse initiale

    Voir la correction

    On projette la vitesse initiale sur les axes Ox (horizontal) et Oy (vertical) : \( V_{0x} = V_0 \cos(\theta) = 25 \times \cos(30°) = 25 \times 0.866 = 21.65 \text{ m/s} \) \( V_{0y} = V_0 \sin(\theta) = 25 \times \sin(30°) = 25 \times 0.5 = 12.5 \text{ m/s} \)

    2. Déterminer l’équation horaire de la trajectoire

    Voir la correction

    Le mouvement horizontal est uniforme : \( x(t) = V_{0x} \cdot t = 21.65 t \) Le mouvement vertical est uniformément accéléré : \( y(t) = V_{0y} \cdot t - \frac{1}{2} g t^2 \) \( y(t) = 12.5 t - 4.905 t^2 \)

    3. Calculer la hauteur maximale atteinte

    Voir la correction

    À l’altitude maximale, la vitesse verticale est nulle : \( t_{h} = \frac{V_{0y}}{g} = \frac{12.5}{9.81} = 1.27 \text{ s} \) \( h_{max} = V_{0y} t_{h} - \frac{1}{2} g t_{h}^2 = 7.93 \text{ m} \) Cette hauteur dépend de l’angle de tir et de la vitesse initiale.

    4. Déterminer la durée totale du vol

    Voir la correction

    En résolvant \( y = 0 \), on obtient : \( t = \frac{2 V_{0y}}{g} = \frac{2 \times 12.5}{9.81} = 2.55 \text{ s} \) Cela signifie que le ballon restera en l’air pendant 2.55 secondes, ce qui influence la stratégie de jeu au football.

    5. Calculer la portée du ballon

    Voir la correction

    \( x_{max} = V_{0x} \times t_{total} = 21.65 \times 2.55 = 55.2 \text{ m} \) L’angle optimal pour une portée maximale est 45° dans l’idéalisation sans frottement.

    6. Discussion sur l’influence de la résistance de l’air

    Voir la correction 

    Marquer comme terminé
• 

  Les sujets hyper classiques :

  • L'architecture des exercices Contenu interactif

    Marquer comme terminé